В частотной области
Среднеквадратичное значение может быть вычислено в частотной области, используя теорему Парсеваля . Для дискретизированного сигнала , где — период дискретизации,
Икспзнак равноИкс(тзнак равнопТ){\ Displaystyle х = х (т = нТ)}Т{\ displaystyle T}
- ∑пзнак равно1NИкс2пзнак равно1N∑мзнак равно1N|Иксм|2,{\ displaystyle \ sum _ {n = 1} ^ {N} {x ^ {2} } = {\ frac {1} {N}} \ sum _ {m = 1} ^ {N} \ left | X \ right | ^ {2},}
где и N — размер выборки, то есть количество наблюдений в выборке и коэффициенты БПФ.
Иксмзнак равноБПФ{Иксп}{\ Displaystyle Х = \ имя оператора {БПФ} \ {х \}}
В этом случае среднеквадратичное значение, вычисленное во временной области, такое же, как и в частотной области:
- RMS{Иксп}знак равно1N∑пИкс2пзнак равно1N2∑м|Иксм|2знак равно∑м|ИксмN|2.{\ displaystyle {\ text {RMS}} \ {x \} = {\ sqrt {{\ frac {1} {N}} \ sum _ {n} {x ^ {2} }} } = {\ sqrt {{\ frac {1} {N ^ {2}}} \ sum _ {m} {{\ bigl |} X {\ bigr |}} ^ {2}}} = { \ sqrt {\ sum _ {m} {\ left | {\ frac {X } {N}} \ right | ^ {2}}}}.}
Действующее и среднее значения переменного тока
Действующее значение переменного тока численно равно такому постоянному току, который, проходя через то же сопротивление, что и переменный ток, выделяет за время, равное 1 периоду, одинаковое количество тепла. Все приборы показывают действующее значение
Если левые части уравнения равны, то и правые будут тоже равны. Приравняв правые части и выполнив операцию интегрирования, получим:
Среднее арифметическое значение переменного тока определяется в течении полупериода; если через поперечное сечение проводника в течении 1 полупериода будет протекать один и тот же заряд при постоянном и переменном токе, то такое значение постоянного тока будет равно среднему значению переменного тока
Среднее значение тока за период равно нулю.
Коэффициенты формы и амплитуды
Отношение действующего значения переменного тока (напряжения или ЭДС) к среднему значению называется коэффициентом формы
, а отношение амплитудного значения к действующему –коэффициентом амплитуды .
Для синусоидального тока:
, а .
Для кривых, имеющих более острую форму, чем синусоида:
;.
Начальная фаза. Сдвиг фаз
| Предположим, что в магнитном поле генератора находится два одинаковых витка, сдвинутых в пространстве друг относительно друга на угол
. При вращении в них буду находится ЭДС одинаковой частоты и амплитуды. |
Но т.к. витки сдвинуты в пространстве, то наводимая в них ЭДС будет достигать амплитудных и нулевых значений не одновременно.
В начальный момент времени
ЭДС витка будет:
В этих выражениях углы
иназываютсяфазными , илифазой . Углыиназываютсяначальной фазой . Фазный угол определяет значение ЭДС в любой момент времени, а начальная фаза определяет значение ЭДС в начальный момент времени.
Разность начальных фаз двух синусоидальных величин одинаковой частоты и амплитуды называется углом сдвига фаз
Разделив угол сдвига фаз на угловую частоту, получим время, прошедшее с начала периода:
| Если угол сдвига фаз составляет 1800, то такие ЭДС находятся в противофазе |
Графическое изображение синусоидальных величин
Синусоидальные величины можно изображать графически при помощи синусоид или вращающихся векторов.
Любая синусоидальная величина характеризуется:
- амплитудой;
- угловой частотой;
- начальной фазой.
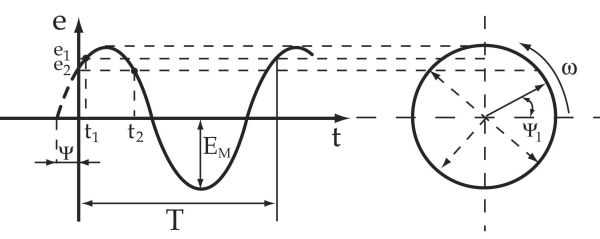
При изображении величины с помощью синусоиды ординаты синусоиды в масштабе представляют собой мгновенное значение, абсциссы – промежутки времени.
При этом длина вектора равна амплитудному значению величины, угол
между положительным направлением оси абсцисс и векторов даст начальную фазу. Вектор вращается против часовой стрелки с угловой скоростью. Проекция конца вектора на ось ординат даст мгновенное значение синусоидальной величины.
Совокупность нескольких синусоид называется синусоидальной (волновой) диаграммой.
Совокупность нескольких векторов называется векторной диаграммой.
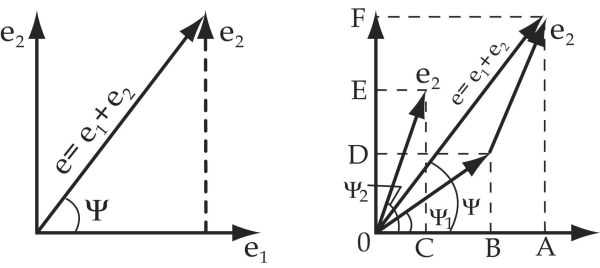
Сложение и вычитание синусоидальных величин
. Для сложения двух синусоидальных величин с помощью синусоид необходимо сложить их ординаты в каждый момент времени.
Для того, чтобы сложить две величины с помощью векторов, необходимо к концу первого вектора добавить второй, не изменяя его величины и направления. Соединив начало первого вектора с концом второго, получим суммарный вектор.
StudFiles.ru
Стандартизация параметров переменного напряжения
Фазное напряжение представляет синусоиду на графике и вращающийся вектор на диаграмме. В идеальном случае. В действительности параметры сети нормируются по ГОСТ 13109, где указаны требования к показателям
Руководствоваться документацией сейчас нужно с осторожностью, по указу правительства страна перешла на фазное напряжение 230 В. Теперь в сети нет 380 В, вместо них – 410 В
Лампочки накала, изготовленные на 220 В, служат меньше в таких условиях. Изменения закреплены в ГОСТ 29322-2014 (IEC 60038-2009).
Проще продемонстрировать фазное напряжение на обычных сетях 220 В. Разница потенциалов между проводами – искомая величина. Фазное напряжение измеряется между линией и схемной землёй. Так дело обстоит в обычной квартире, но на производстве иначе. Там каждая фаза рассматривается в совокупности с прочими. Нейтраль порой отсутствует. Тогда напряжение между фазами называют линейным. Фазное вводится для распознавания типа сети (наличие нейтрали).
Новый ГОСТ 29322 вводит понятие сетей 60 Гц. Фаз предусмотрено две или три. Тогда указываются две цифры. К примеру, 230/400 или 120/240. Легко заметить, что отношения между цифрами в каждой паре разные. Фазные напряжения указаны на первом месте, линейные – через дробь. Это помогает уточнить топологию. Сети по структуре неодинаковы, фазное напряжение позволяет судить об этом точно.
Если указана пара 230/400 В, электрик сразу видит, что отношение цифр равняется корню из трёх. Значит, система трёхфазная. Тогда ищут дополнительные сведения – изолированная нейтраль либо глухозаземлённая. Что касается цифр 120/240, уточнив частоту (60 Гц), возможно с определённостью сказать, что это однофазная сеть с топологией из трёх проводов. Фазы подаются через трансформатор (допустим) с нейтралью в общей точке. Подобная схема применялась в довоенной Германии и кое-где используется поныне. В последнем случае применяются при необходимости двухполюсные автоматы.
В связи со сказанным заметим, что номинал напряжения поменялся, но ГОСТ 13109 не учёл пока означенного факта. Там обсуждается устаревшее ныне значение 380 В. Впрочем, параметрами допустимо руководствоваться для определённых случаев. ГОСТ 13109 числится как действующий, параллельно введён дополнительный документ – ГОСТ Р 54149. Документ нормирует допуски, как:
- Отклонение амплитуды напряжения – 5 – 10% в каждую сторону в зависимости от отдельно взятого случая.
- Колебания напряжения.
- Несинусоидальность.
- Несимметрия (для многофазных цепей).
- Отклонение частоты от 0,2 до 0,4 Гц и пр.
Легко заметить, что самые жёсткие требования предъявляются к частоте. Это важнейший параметр фазного напряжения. Новый ГОСТ Р 54149 вводит понятия асинхронных систем передачи энергии, где требования к частоте заметно мягче. Допускаются отклонения частоты в 1 Гц в 95% времени. В течение оставшихся 5% допускается отклонение по 5 Гц в каждую сторону.
Указанные значения, видимо, связаны с линиями передач, потому что сегодня редко встречается оборудование, неспособное противостоять скачкам по частоте. К примеру, большая часть двигателей управляется напряжением. С ростом переменой частоты негативно изменяется реактивное сопротивление сети. Точнее – увеличивается его индуктивная составляющая и уменьшается ёмкостная, усугубляя обстановку. Индуктивную часть и так стремятся компенсировать включением блоков конденсаторов для снижения реактивной мощности.
Среднеквадратичное значение
|
Определение среднего времени пересечения ячейки на участке годографа пространственных частот, показанного штриховой линией. Скорость вектора базы на плоскости u v равна u eq. Средняя длина пути через ячейку в направлении штриховой линии равна площади ячейки Аи Аи, деленной на ее ширину, спроецированную на нормаль к этому направлению. |
Для определения среднеквадратичного значения Д используем простое приближение, суть которого состоит в рассмотрении изменения этой величины на плоскости м г /, когда вектор базы вращается с постоянной скоростью ( jje и им описывается окружность, как показано в разд. Тогда эффективное время усреднения т для помехи равно времени, за которое ячейка пересекается вектором базы, как показано на рис. 15.3. Заметим, что как следует из формулы (15.4), величина частоты интерференции равна нулю на оси г /, и в этом случае Д равно единице.
|
Зависимости среднеквадратичных значений пульсационных составляющих компонент скоростей частиц от диаметра частиц ( D 220 мм, Г 0 6. / — Г1 15 м / с. 2 — W2 0 м / с. 3 — W3 6 м / с.| Корреляционный график для среднеквадратичных значений акси. |
Сравнение зависимостей среднеквадратичных значений пульсационных составляющих аксиальной и радиальной компонент скорости частиц от параметров псевдоожижения показывает, что эти зависимости для обеих компонент имеют одинаковый характер. Одинаковый характер изменения компонент объясняется устойчивой связью между значениями аксиальной и радиальной компонент пульсационной составляющей скорости частиц при всех режимах псевдоожижения.
|
Подключение микроамперметра при регулировке напряжения на аноде кинескопа ( а и эквивалент нагрузки обмотки подогревателя ТВС при проверке напряжения накала кинескопа ( б. |
Для проверки среднеквадратичного значения напряжения накала ( табл. 5.1) используется прибор типа ВЗ-48.
Электростатические вольтметры измеряют истинное среднеквадратичное значение в вольтах. Они также могут быть использованы для измерения пиковых напряжений в соединении с выпрямителем, через который емкость заряжается до пикового значения напряжения.
|
Нагрузочный ток тяговой подстанции. |
Максимальные значения превышают соответствующие среднеквадратичные значения в 1 77 -: — — 2 76 раза.
В этом приближении среднеквадратичное значение угла, под которым испускается излучение, определяется той же формулой (14.42), что и при одномерном движении.
Средняя чувствительность — среднеквадратичное значение чувствительности в номинальном диапазоне частот микрофона; усредняют по значениям на частотах, распределенных равномерно в логарифмическом масштабе.
Полнее характеризует напряжение среднеквадратичное значение U. Его еще называют эффективным i / эфф или действующим t / девст значением переменного напряжения или тока.
Тепловой амперметр дает среднеквадратичное значение измеряемого тока. Шкала этого прибора нелинейна. Центральная отметка шкалы составляет 1 / 1 / 2 полного отклонения шкалы или 0 707 от величины соответствующей всей шкале. Но вследствие того, что этот ток изменяется пропорционально квадрату приложенного напряжения, два квадратичных закона взаимно компенсируются и шкала, градуированная в ваттах, линейна.
Показать, что среднеквадратичное значение случайной ошибки системы не зависит от постоянной времени фильтра.
Таким образом, среднеквадратичное значение флуктуации интенсивности равно средней интенсивности; иными словами, контраст случайной интерференционной картины является действительно очень высоким.
Период пульсаций и частота
Физическая сущность переменного тока заключается в перемещении электронов в проводнике сначала в одном направлении, затем в другую сторону. Полный цикл движений туда и обратно совершается за определённый период, определяемый по частоте колебаний: Т=1/ f.
Интенсивность циклов
Для условий электросетей России показатель f =50 Гц, а время одной пульсации составляет Т=1/50=0,02 секунды. Обратная связь двух параметров позволяет определить частоту ~ тока по длительности сигнала: f =1/0,02=50 Гц.
Один герц означает 1 колебание за секунду. Чем быстрее изменяется электродвижущая сила, тем скорее обращается радиус-вектор и сокращается период. Соответственно, при форсировании оборотов возрастает частота: величины Т и f обратно пропорциональны, чем больше одна, тем меньше вторая. Значения характеристики f изменяются в широких пределах, что предопределяет использование расширенной терминологии:
| Количество нулей после единицы | Приставка к размерности герц |
| 3 (тысяча) | Кило (кГц) |
| 6 (миллион) | Мега (мГц) |
| 9 (миллиард) | Гига (ГГц) |
В зависимости от величины частота переменного тока подразделяется на следующие подгруппы:
- промышленные: 16―25 Гц на железнодорожных сетях некоторых стран, 25 и 75 Гц в схемах блокировки рельсовых цепей, в автономных системах авиационной и военной энергетики — 400 Гц, на некоторых производственных и сельскохозяйственных установках 200―400 Гц;
- звуковые находятся в интервале 20―20000 Гц (20 кГц), в передающих антеннах — до 1,5 ГГц;
- технические: автоматика — используется диапазон от 1 кГц до 1 ГГц, металлургия и машиностроение: плавка, сварка и термообработка металлов;
- радиолокационные станции спутниковой связи, спецсистемы ГЛОНАСС, GPS — до 40 ГГц и выше.
Токи высокой частоты (ТВЧ) начинаются с уровня десятков кГц, когда значимо проявляются излучения электромагнитных волн и скин-эффект: заряд, перемещающийся в проводнике, распределяется не по сечению, а в поверхностном слое.
Опасность разночастотных зарядов
Эквивалентные по воздействию на организм человека напряжения переменного и постоянного тока, равны соответственно 42 В и 120 В. Неравенство опасности исчезает при достижении ЭДС 500 В, а при больших значениях опаснее становится константный. Проявления неблагоприятного действия последнего — термическое и электролитическое, а переменного — преимущественно выражается в сокращении сосудов, мышц, голосовых связок. При этом определяющее значение на опасность оказывает частота тока:
- 40―60 Гц — наибольшая угроза поражения, возможность фибрилляции сердца; дальнейшее повышение интенсивности колебаний зарядов приводит к снижению риска, но вероятность гибельности сохраняется в пределах всего диапазона промышленных частот — до 500 Гц;
- свыше 10 кГц начинаются ТВЧ — они безопасны до уровня 1 мГц относительно внутренних поражений, что обусловлено скин-эффектом, но вызывают ожог и угроза от них не меньше, чем от постоянных или переменных предшествующей группы;
- токи высокой частоты сопровождаются электромагнитными излучениями — с этой стороны существует возможность негативного воздействия на живые организмы.
Советуем изучить Стабилизатор напряжения на транзисторе
Понятие выборочного наблюдения и область его применения.
Выборочное наблюдение применяется, когда применение сплошного наблюдения физически невозможно из-за большого массива данных или экономически нецелесообразно. Физическая невозможность имеет место, например, при изучении пассажиропотоков, рыночных цен, семейных бюджетов. Экономическая нецелесообразность имеет место при оценке качества товаров, связанной с их уничтожением, например, дегустация, испытание кирпичей на прочность и т.п.
Статистические единицы, отобранные для наблюдения, составляют выборочную совокупность или выборку, а весь их массив – генеральную совокупность (ГС). При этом числоединиц ввыборке обозначают n, а во всей ГС – N. Отношение n/N называется относительныйразмер или долявыборки.
Качество результатов выборочного наблюдения зависит от репрезентативности выборки, то есть от того, насколько она представительна в ГС. Для обеспечения репрезентативности выборки необходимо соблюдать принцип случайности отбора единиц, который предполагает, что на включение единицы ГС в выборку не может повлиять какой-либо иной фактор кроме случая.
Существует 4 способа случайного отбора в выборку:
- Собственно случайный отбор или «метод лото», когда статистическим величинам присваиваются порядковые номера, заносимые на определенные предметы (например, бочонки), которые затем перемешиваются в некоторой емкости (например, в мешке) и выбираются наугад. На практике этот способ осуществляют с помощью генератора случайных чисел или математических таблиц случайных чисел.
- Механический отбор, согласно которому отбирается каждая (N/n)-я величина генеральной совокупности. Например, если она содержит 100 000 величин, а требуется выбрать 1 000, то в выборку попадет каждая 100 000 / 1000 = 100-я величина. Причем, если они не ранжированы, то первая выбирается наугад из первой сотни, а номера других будут на сотню больше. Например, если первой оказалась единица № 19, то следующей должна быть № 119, затем № 219, затем № 319 и т.д. Если единицы генеральной совокупности ранжированы, то первой выбирается № 50, затем № 150, затем № 250 и так далее.
- Отбор величин из неоднородного массива данных ведется стратифицированным (расслоенным) способом, когда генеральная совокупность предварительно разбивается на однородные группы, к которым применяется случайный или механический отбор.
- Особый способ составления выборки представляет собой серийный отбор, при котором случайно или механически выбирают не отдельные величины, а их серии (последовательности с какого-то номера по какой-то подряд), внутри которых ведут сплошное наблюдение.
Качество выборочных наблюдений зависит и от типа выборки: повторная или бесповторная.
При повторном отборе попавшие в выборку статистические величины или их серии после использования возвращаются в генеральную совокупность, имея шанс попасть в новую выборку. При этом у всех величин генеральной совокупности одинаковая вероятность включения в выборку.
Бесповторный отбор означает, что попавшие в выборку статистические величины или их серии после использования не возвращаются в генеральную совокупность, а потому для остальных величин последней повышается вероятность попадания в следующую выборку.
Бесповторный отбор дает более точные результаты, поэтому применяется чаще. Но есть ситуации, когда его применить нельзя (изучение пассажиропотоков, потребительского спроса и т.п.) и тогда ведется повторный отбор.
В распространенных формах волны
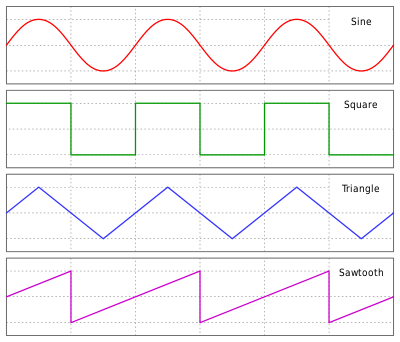
Синусоидальные , квадратные , треугольные и пилообразные формы сигналов. В каждом из них центральная линия находится на 0, положительный пик — на, а отрицательный — наузнак равноА1{\ displaystyle y = A_ {1}}узнак равно-А1{\ displaystyle y = -A_ {1}}
Прямоугольная импульсная волна с коэффициентом заполнения D, соотношением длительности импульса ( ) и периода (T); проиллюстрировано здесь с a = 1.τ{\ Displaystyle \ тау}
График зависимости напряжения синусоидальной волны от времени (в градусах), показывающий среднеквадратичное, пиковое (PK) и размах напряжения (PP).
Если форма волны представляет собой чистую синусоидальную волну , отношения между амплитудами (размах, пик) и среднеквадратичным значением фиксированы и известны, как и для любой непрерывной периодической волны. Однако это неверно для сигнала произвольной формы, который не может быть периодическим или непрерывным. Для синусоидальной волны с нулевым средним соотношение между среднеквадратичным значением и размахом амплитуды составляет:
- От пика до пика знак равно22×RMS≈2,8×RMS.{\ displaystyle = 2 {\ sqrt {2}} \ times {\ text {RMS}} \ примерно 2,8 \ times {\ text {RMS}}.}
Для других сигналов отношения не такие же, как для синусоидальных волн. Например, для треугольной или пилообразной волны
- От пика до пика знак равно23×RMS≈3.5×RMS.{\ displaystyle = 2 {\ sqrt {3}} \ times {\ text {RMS}} \ примерно 3,5 \ times {\ text {RMS}}.}
| Форма волны | Переменные и операторы | RMS |
|---|---|---|
| ОКРУГ КОЛУМБИЯ | узнак равноА{\ displaystyle y = A_ {0} \,} | А{\ displaystyle A_ {0} \,} |
| Синусоидальная волна | узнак равноА1грех(2πжт){\ Displaystyle у = А_ {1} \ грех (2 \ пи футов) \,} | А12{\ displaystyle {\ frac {A_ {1}} {\ sqrt {2}}}} |
| Квадратная волна | узнак равно{А1гидроразрыв(жт)<0,5-А1гидроразрыв(жт)>0,5{\ displaystyle y = {\ begin {cases} A_ {1} & \ operatorname {frac} (ft) <0,5 \\ — A_ {1} & \ operatorname {frac} (ft)> 0,5 \ end {cases}} } | А1{\ Displaystyle A_ {1} \,} |
| Прямоугольная волна со смещением постоянного тока | узнак равноА+{А1гидроразрыв(жт)<0,5-А1гидроразрыв(жт)>0,5{\ displaystyle y = A_ {0} + {\ begin {cases} A_ {1} & \ operatorname {frac} (ft) <0,5 \\ — A_ {1} & \ operatorname {frac} (ft)> 0,5 \ конец {case}}} | А2+А12{\ displaystyle {\ sqrt {A_ {0} ^ {2} + A_ {1} ^ {2}}} \,} |
| узнак равно{гидроразрыв(жт)<0,25А10,25<гидроразрыв(жт)<0,50,5<гидроразрыв(жт)<0,75-А1гидроразрыв(жт)>0,75{\ displaystyle y = {\ begin {cases} 0 & \ operatorname {frac} (ft) <0,25 \\ A_ {1} & 0,25 <\ operatorname {frac} (ft) <0,5 \\ 0 & 0,5 <\ operatorname {frac} (ft) <0,75 \\ — A_ {1} & \ operatorname {frac} (ft)> 0,75 \ end {case}}} | А12{\ displaystyle {\ frac {A_ {1}} {\ sqrt {2}}}} | |
| Треугольник волна | узнак равно|2А1гидроразрыв(жт)-А1|{\ displaystyle y = \ left | 2A_ {1} \ operatorname {frac} (ft) -A_ {1} \ right |} | А13{\ displaystyle A_ {1} \ over {\ sqrt {3}}} |
| Пилообразная волна | узнак равно2А1гидроразрыв(жт)-А1{\ displaystyle y = 2A_ {1} \ operatorname {frac} (ft) -A_ {1} \,} | А13{\ displaystyle A_ {1} \ over {\ sqrt {3}}} |
| Пульсовая волна | узнак равно{А1гидроразрыв(жт)<Dгидроразрыв(жт)>D{\ displaystyle y = {\ begin {cases} A_ {1} & \ operatorname {frac} (ft) <D \\ 0 & \ operatorname {frac} (ft)> D \ end {cases}}} | А1D{\ displaystyle A_ {1} {\ sqrt {D}}} |
| Междуфазное напряжение | узнак равноА1грех(т)-А1грех(т-2π3){\ displaystyle y = A_ {1} \ sin (t) -A_ {1} \ sin \ left (t — {\ frac {2 \ pi} {3}} \ right) \,} | А132{\ displaystyle A_ {1} {\ sqrt {\ frac {3} {2}}}} |
куда:
|
В комбинациях сигналов
Формы сигналов, полученные путем суммирования известных простых сигналов, имеют среднеквадратичное значение, которое является корнем из суммы квадратов значений компонентных среднеквадратичных значений, если формы сигналов компонентов ортогональны (то есть, если среднее произведение одного простого сигнала на другой равно нулю. для всех пар, кроме самого времени сигнала).
- RMSОбщийзнак равноRMS12+RMS22+⋯+RMSп2{\ displaystyle {\ text {RMS}} _ {\ text {Total}} = {\ sqrt {{\ text {RMS}} _ {1} ^ {2} + {\ text {RMS}} _ {2} ^ {2} + \ cdots + {\ text {RMS}} _ {n} ^ {2}}}}
В качестве альтернативы, для сигналов, которые полностью положительно коррелированы или «синфазны» друг с другом, их среднеквадратичные значения суммируются напрямую.
Свойства дисперсии
Свойство 1. Дисперсия постоянной величины A равна (нулю).
D(A) = 0
Свойство 2. Если случайную величину умножить на постоянную А, то дисперсия этой случайной величины увеличится в А2 раз. Другими словами, постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат.
D(AX) = А2 D(X)
Свойство 3. Если к случайной величине добавить (или отнять) постоянную А, то дисперсия останется неизменной.
D(A + X) = D(X)
Свойство 4. Если случайные величины X и Y независимы, то дисперсия их суммы равна сумме их дисперсий.
D(X+Y) = D(X) + D(Y)
Свойство 5. Если случайные величины X и Y независимы, то дисперсия их разницы также равна сумме дисперсий.
D(X-Y) = D(X) + D(Y)
RMS против среднего
Чтобы понять разницу между среднеквадратичным и средним значением, необходимо знать, что такое среднее (или среднее значение), а что такое среднеквадратичное значение (среднеквадратичное значение). Среднеквадратичное значение и Среднее значение — это два математических понятия, используемых для описания общей природы набора чисел. Использование распространяется на физические науки и связанные с ними технологии в том же контексте. Среднее значение — это довольно знакомая и интуитивно понятная концепция, в то время как RMS — это концепция, явно основанная на математическом определении. Давайте подробно рассмотрим их определения и методы расчета среднего и среднеквадратичного значений.
Что такое среднее (или среднее) значение?
В математике среднее — это суммирование ряда значений, чтобы дать общее представление о коллекции. Он также используется в качестве описательной статистики, следовательно, считается мерой центральной тенденции.
Среднее значение рассчитывается разными способами в зависимости от приложения. Поэтому точное математическое определение среднего значения варьируется: это среднее арифметическое, среднее геометрическое, гармоническое среднее и взвешенное среднее. Их определения следующие.
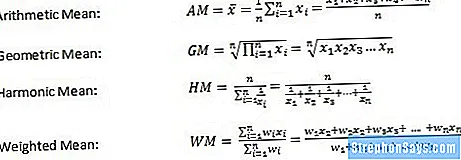
куда Икся представляют значения данных и шя — вес каждого значения. Стоит отметить, что AM, GM и HM удовлетворяют следующей неопределенности: AM≥GM≥HM.
Средневзвешенное значение можно рассматривать как расширение среднего арифметического. Усеченное среднее, межквартильное среднее и выигрышное среднее также используются в конкретных случаях, но наиболее часто используются первые три типа средних, известные как средние по Пифагору.
Что такое RMS — среднеквадратическое значение?
В некоторых приложениях простые пифагоровы средние не являются точным указанием выборки данных. Например, рассмотрим изменяющийся во времени синусоидальный электронный сигнал без сдвига напряжения. Среднее значение амплитуды в пределах цикла равно нулю, что означает, что напряжение в течение этого периода было нулевым, что физически неверно. В результате любые вычисления, включающие значения, неверны.
Например, рассчитанная энергия дает неверные значения. Если рассматривать максимальные или минимальные значения сигнала, ответы все равно являются отдаленным признаком разумного. Анализируя первопричину, становится очевидным, что колебания от отрицательного к положительному приводит к тому, что значения компенсируют друг друга, когда они суммируются. Следовательно, значения должны добавляться таким образом, чтобы они не отменяли друг друга.
В качестве альтернативы можно рассматривать квадратичное среднее или среднеквадратичные значения. Среднеквадратичное значение определяется как,
Поскольку каждое значение возведено в квадрат, все значения положительны, и отмены чередующихся значений предотвращается.
Напряжение и ток в электросети в наших домах указывают на действующие значения напряжений и тока переменного напряжения источника. Идею среднего квадрата можно распространить на более общий случай (все символы имеют обычное значение):
В чем разница между среднеквадратичным и средним (средним) значением?
Среднее — это обобщение набора чисел, которое является мерой центральной тенденции для выборки населения, и это важная описательная статистика.
Среднее значение определяется математически по-разному, и интерпретация наиболее верна в зависимости от приложения.
Среднее арифметическое — это сумма всех рассмотренных значений данных, деленная на количество значений данных, что дает одно число для представления всего набора данных. Когда есть как отрицательные, так и положительные числа, они отменяются, и в зависимости от сценария это значение может не представлять набор данных допустимым образом.
В качестве среднего арифметического берется сумма значений данных без каких-либо изменений.
В RMS значения данных возводятся в квадрат, и после вычисления среднего арифметического этих квадратов значений извлекается квадратный корень из этого числа.
Что такое RMS
Среднеквадратичные значения получаются в результате математической процедуры, используемой для расчета единичного значения по последовательности отсчетов. Это позволяет сравнивать один цикл с другим, или одну фазу с другой. RMS-напряжение является эффективным значением изменяющегося или переменного напряжения. Это значение должно соответствовать такой же мощности, как и в случае постоянного напряжения, приложенного к чистому сопротивлению. В нынешнем мире дискретных волновых сигналов, вырабатываемых кристаллами процессоров цифровой обработки сигнала (ЦОС), такие измерения являются одними из наиболее легко реализуемых. Каждое значение данных в течение предопределенного периода (обычно это один цикл) умножается само на себя (возведение в квадрат), а затем все такие значения в течение периода усредняются (суммируются с последующим делением на общее количество) и из полученного значения извлекается квадратный корень.
Для стабильного постоянного сигнала каждый отсчет имеет одно и то же значение, следовательно, любой из них может служить эквивалентом RMS-значения. В случае же синусоидальной волны значения нарастают в пределах первой четверти цикла, затем уменьшаются до нуля и переходят в область отрицательных значений вплоть до минимального значения в пределах второй четверти цикла .
Мгновенная мощность в цепи переменного тока с активным сопротивлением.
При переменных величинах напряжения и тока скорость преобразования электрической энергии в приемнике, т. е. его мощность, тоже изменяется. Мгновенная мощность равна произведению мгновенных величин напряжения и тока: p = Umsinωt * Imsinωt = UmImsin2ωt
Из тригонометрии найдём
Более наглядное представление о характере изменения мощности в цепи дает график в прямоугольной системе координат, который строится после умножения ординат кривых напряжения и тока, соответствующих ряду значений их общего аргумента — времени t. Зависимость мощности от времени — периодическая кривая (рис. 13.2). Если ось времени t поднять по чертежу на величину р = Pm√2 = UmIm√2, то относительно новой оси t’ график мощности является синусоидой с двойной частотой и начальной фазой 90°:
Таким образом, в первоначальной системе координат мгновенная, мощность равна сумме постоянной величины Р = UmIm√2 и перемен- ной р’:
р = Р + р’
Анализируя график мгновенной мощности, нетрудно заметить, что мощность в течение периода остается положительной, хотя ток и напряжение меняют свой знак. Это получается благодаря совпадению по фазе напряжения и тока.
Постоянство знака мощности говорит о том, что направление потока электрической энергии остается в течение периода неизменным, в данном случае от сети (от источника энергии) в приемник с сопротивлением R, где электрическая энергия необратимо преобразуется в другой вид энергии. В этом случае электрическая энергия называется активной.
Советуем изучить Ремонт датчика движения своими руками
Если R — сопротивление проводника, то в соответствии с законом Ленца — Джоуля электрическая энергия в нем преобразуется в тепло.
Шаги
Часть 1 из 3:
Среднее значение
-
1
Возьмите наборе данных. Среднее значение – это важная величина в статистических расчетах.
X
Источник информации- Определите количество чисел в наборе данных.
- Числа в наборе сильно отличаются друг от друга или они очень близки (отличаются на дробные доли)?
- Что представляют числа в наборе данных? Тестовые оценки, показания пульса, роста, веса и так далее.
- Например, набор тестовых оценок: 10, 8, 10, 8, 8, 4.
-
2
Для вычисления среднего значения понадобятся все числа данного набора данных.
X
Источник информации- Среднее значение – это усредненное значение всех чисел в наборе данных.
- Для вычисления среднего значения сложите все числа вашего набора данных и разделите полученное значение на общее количество чисел в наборе (n).
- В нашем примере (10, 8, 10, 8, 8, 4) n = 6.
-
3
Сложите все числа вашего набора данных.
X
Источник информации- В нашем примере даны числа: 10, 8, 10, 8, 8 и 4.
- 10 + 8 + 10 + 8 + 8 + 4 = 48. Это сумма всех чисел в наборе данных.
- Сложите числа еще раз, чтобы проверить ответ.
-
4
Разделите сумму чисел на количество чисел (n) в выборке. Вы найдете среднее значение.
X
Источник информации- В нашем примере (10, 8, 10, 8, 8 и 4) n = 6.
- В нашем примере сумма чисел равна 48. Таким образом, разделите 48 на n.
- 48/6 = 8
- Среднее значение данной выборки равно 8.
Часть 2 из 3:
Дисперсия
1
Вычислите дисперсию. Это мера разброса данных вокруг среднего значения.
X
Источник информации
Эта величина даст вам представление о том, как разбросаны данные выборки.
Выборка с малой дисперсией включает данные, которые ненамного отличаются от среднего значения.
Выборка с высокой дисперсией включает данные, которые сильно отличаются от среднего значения.
Дисперсию часто используют для того, чтобы сравнить распределение двух наборов данных.
2
Вычтите среднее значение из каждого числа в наборе данных. Вы узнаете, насколько каждая величина в наборе данных отличается от среднего значения.
X
Источник информации
В нашем примере (10, 8, 10, 8, 8, 4) среднее значение равно 8.
10 — 8 = 2; 8 — 8 = 0, 10 — 2 = 8, 8 — 8 = 0, 8 — 8 = 0, и 4 — 8 = -4.
Проделайте вычитания еще раз, чтобы проверить каждый ответ
Это очень важно, так как полученные значения понадобятся при вычислениях других величин. 3
3
Возведите в квадрат каждое значение, полученное вами в предыдущем шаге.
X
Источник информации
При вычитании среднего значения (8) из каждого числа данной выборки (10, 8, 10, 8, 8 и 4) вы получили следующие значения: 2, 0, 2, 0, 0 и -4.
Возведите эти значения в квадрат: 22, 02, 22, 02, 02, и (-4)2 = 4, 0, 4, 0, 0, и 16.
Проверьте ответы, прежде чем приступить к следующему шагу.
4
Сложите квадраты значений, то есть найдите сумму квадратов.
X
Источник информации
В нашем примере квадраты значений: 4, 0, 4, 0, 0 и 16.
Напомним, что значения получены путем вычитания среднего значения из каждого числа выборки: (10-8)^2 + (8-8)^2 + (10-2)^2 + (8-8)^2 + (8-8)^2 + (4-8)^2
4 + 0 + 4 + 0 + 0 + 16 = 24.
Сумма квадратов равна 24.
5
Разделите сумму квадратов на (n-1). Помните, что n – это количество данных (чисел) в вашей выборке
Таким образом, вы получите дисперсию.
X
Источник информации
В нашем примере (10, 8, 10, 8, 8, 4) n = 6.
n-1 = 5.
В нашем примере сумма квадратов равна 24.
24/5 = 4,8
Дисперсия данной выборки равна 4,8.
Часть 3 из 3:
Среднеквадратическое отклонение
-
1
Найдите дисперсию, чтобы вычислить среднеквадратическое отклонение.
X
Источник информации- Помните, что дисперсия – это мера разброса данных вокруг среднего значения.
- Среднеквадратическое отклонение – это аналогичная величина, описывающая характер распределения данных в выборке.
- В нашем примере дисперсия равна 4,8.
-
2
Извлеките квадратный корень из дисперсии, чтобы найти среднеквадратическое отклонение.
X
Источник информации- Как правило, 68% всех данных расположены в пределах одного среднеквадратического отклонения от среднего значения.
- В нашем примере дисперсия равна 4,8.
- √4,8 = 2,19. Среднеквадратическое отклонение данной выборки равно 2,19.
- 5 из 6 чисел (83%) данной выборки (10, 8, 10, 8, 8, 4) находится в пределах одного среднеквадратического отклонения (2,19) от среднего значения (8).
-
3
Проверьте правильность вычисления среднего значения, дисперсии и среднеквадратического отклонения. Это позволит вам проверить ваш ответ.
X
Источник информации- Обязательно записывайте вычисления.
- Если в процессе проверки вычислений вы получили другое значение, проверьте все вычисления с самого начала.
- Если вы не можете найти, где сделали ошибку, проделайте вычисления с самого начала.






