Что такое потенциал и разность потенциалов между двумя точками

1.5. Электрокардиография. Теория отведений Эйнтховена.

При функционировании тканей,
органов и отдельных клеток, сопровождающемся электрической активностью, в
организме создается электрическое поле. Поэтому два электрода, наложенные на
разные участки тела, регистрирует разность потенциалов. Зависимость этой
разницы потенциалов от времени называется электрограммой. Названия
электрограмм указывают на органы (ткани), функционирование которых приводит к
появлению регистрируемой разности потенциалов: электрокардиограмма (ЭКГ),
электроэнцефаллограмма (ЭЭГ), электромиограмма (ЭМГ) и т.д.

Можно сформулировать
две основные задачи изучения электрограмм: первая заключается в выяснении
механизма их возникновения, вторая — в выяснении состояния органа по характеру
его электрограммы. Наибольшее распространение получило использование электрокардиограмм
(ЭКГ), дающих сведения о состоянии и работе сердца.

Эквипотенциальные поверхности

Если потенциал нескольких точек одинаков, и эти точки образуют поверхность, то такая поверхность называется эквипотенциальной. Таким свойством обладает, например, сфера, описанная вокруг электрического заряда, ведь электрическое поле убывает с расстоянием одинаково во все стороны.

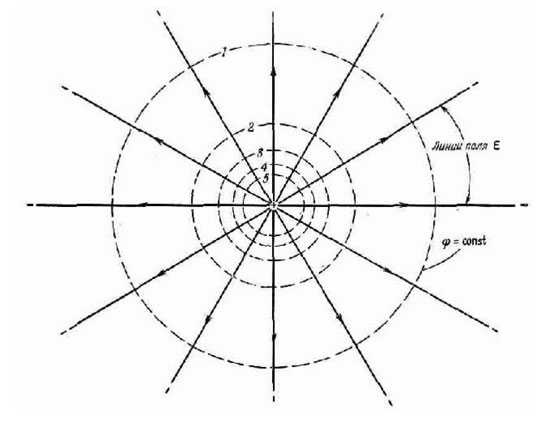
Все точки этой поверхности имеют одинаковую потенциальную энергию, поэтому при перемещении заряда по такой сфере работа затрачиваться не будет. Эквипотенциальные поверхности систем из нескольких зарядов имеют более сложную форму, но у них есть одно интересное свойство – они никогда не пересекаются. Силовые линии электрического поля всегда перпендикулярны поверхностям с одинаковым потенциалом в каждой их точке. Если эквипотенциальную поверхность рассечь плоскостью, получится линия равных потенциалов. Она имеет те же свойства, что и эквипотенциальная поверхность. На практике равный потенциал имеют, например, точки на поверхности проводника, помещенного в электростатическое поле.

Разобравшись с понятием потенциала и разности потенциалов, можно приступать к дальнейшему изучению электрических явлений. Но не ранее, потому что без понимания базовых принципов и понятий углубить знания не получится.

Что такое диэлектрическая проницаемость

Что такое электрофорная машина и как она работает?

Что такое электрический ток простыми словами

Что такое шаговое напряжение и как покинуть опасную зону

Что такое электрическая ёмкость, в чём измеряется и от чего зависит

Сила Лоренца и правило левой руки. Движение заряженных частиц в магнитном поле

Что такое электрический потенциал

Пусть в поле, создаваемым неподвижным зарядом Q, помещён единичный заряд q, на который действует сила Кулона F=k*Qq/r.

Внесённый заряд под действием этой силы может перемещаться, а сила при этом совершит определенную работу. Это означает, что система из двух зарядов обладает потенциальной энергией, зависящей от величины обоих зарядов и расстояния между ними, причём величина этой потенциальной энергии не зависит от величины заряда q. Здесь и вводится определение электрического потенциала – он равен отношению потенциальной энергии поля к величине заряда:

φ=W/q,

где W – потенциальная энергия поля, создаваемого системой зарядов, а потенциал является энергетической характеристикой поля. Чтобы переместить заряд q в электрическом поле на какое-то расстояние, надо затратить определённую работу на преодоление кулоновских сил. Потенциал точки равен работе, которую надо затратить для перемещения единичного заряда из этой точки в бесконечность. При этом надо отметить, что:

эта работа будет равна убыли потенциальной энергии заряда (A=W₂-W₁);
работа не зависит от траектории перемещения заряда.

В системе СИ единицей измерения потенциала является один Вольт (в русскоязычной литературе обозначается буквой В, в зарубежной – V). 1 В=1Дж/1 Кл, то есть, можно говорить о потенциале точки в 1 вольт, если для перемещения заряда в 1 Кл в бесконечность потребуется совершить работу в 1 Джоуль. Название выбрано в честь итальянского физика Алессандро Вольта, внесшего значительный вклад в развитие электротехники.

Чтобы наглядно представить, что такое потенциал, его можно сравнить с температурой двух тел или температурой, замеренной в разных точках пространства. Температура служит мерой нагрева объектов, а потенциал – мерой электрической заряженности. Говорят, что одно тело нагрето более другого, также можно сказать, что одно тело заряжено более, а другое – менее. Эти тела обладают разным потенциалом.

Значение потенциала зависит от выбора системы координат, поэтому требуется какой-то уровень, который надо принять за ноль. При измерении температуры за базовую границу можно принять, например, температуру тающего льда. Для потенциала за нулевой уровень обычно принимают потенциал бесконечно удаленной точки, но для решения некоторых задач за нулем можно считать, например, потенциал земли или потенциал одной из обкладок конденсатора.

1.4. Дипольный эквивалентный электрический генератор сердца.

В возбужденном миокарде
всегда имеются много диполей (назовем их элементарными). Потенциал поля каждого
диполя в неограниченной среде подчиняется уравнению:

,
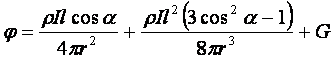где (13)

G – сумма
членов, которые пропорциональны l3/r4, l4/r5 и т.д.

j
— потенциал в точке регистрации, l – величина диполя,

I – сила
тока, r — удельное сопротивление среды
(рис.7).

Рис.7. Элементарный диполь.

При изучении
потенциалов на значительном удалении от сердца, когда выполняется условие r>>l, первый член правой части уравнения (13) намного
превосходит остальные. Поэтому в первом приближении вторым и последующими
членами можно пренебречь. Это заведомо справедливо в случае точечных диполей, у
которых l0.
Первый член в правой части уравнения (13) именуют дипольным потенциалом
(потенциалом точечного диполя).

Потенциал (j) электрического поля сердца
складывается из дипольных потенциалов элементарных диполей. Поскольку в каждый
момент кардиоцикла возбуждается сравнительно небольшой участок миокарда,
расстояния от всех диполей до точки измерения потенциала примерно равны друг
другу, и j приближенно
описывается уравнением:

,
(14)

в котором r – одинаковое для всех диполей расстояние до точки измерения
потенциала, m – количество диполей. Сумму проекций в
этом выражении можно рассматривать как проекцию вектора дипольного момента () одного токового диполя, у которого

.
(15)

Этот диполь
называют эквивалентным диполем сердца. Таким образом, потенциал внешнего
электрического поля сердца можно представить в виде дипольного потенциала
одного эквивалентного диполя:

,
(16)

где a — угол между и
направлением регистрации потенциала; D –
модуль вектора .

Модель, в
которой электрическая активность миокарда заменяется действием одного точечного
диполя и потенциалы внешнего поля описываются выражением (11) называют дипольным
эквивалентным электрическим генератором сердца.

Свойства потенциала

Среди важных свойств потенциала надо отметить следующие:

если поле создается несколькими зарядами, то потенциал в конкретной точке будет равен алгебраической (с учетом знака заряда) сумме потенциалов, создаваемых каждым из зарядов φ=φ₁+φ₂+φ₃+φ₄+φ₅+…+φ_n;
если расстояния от зарядов таковы, что сами заряды можно считать точечными, то суммарный потенциал считается по формуле φ=k*(q₁/r₁+q₂/r₂+q₃/r₃+…+q_n/r_n), где r – расстояние от соответствующего заряда то рассматриваемой точки.

Если поле образовано электрическим диполем (двумя связанными зарядами противоположного знака), то потенциал в любой точке, находящейся на расстоянии r от диполя будет равен φ=k*p*cosά/r2, где:

p – электрическое плечо диполя, равное q*l, где l – расстояние между зарядами;
r – расстояние до диполя;
ά – угол между плечом диполя и радиус-вектором r.

Если точка лежит на оси диполя, то cosά=1 и φ=k*p/r2.

Поле колеблющегося диполя

В этом разделе рассматривается поле, создаваемое точечным электрическим диполем d(t),{\displaystyle \mathbf {d} (t),} находящимся в заданной точке пространства.

Поле на близких расстояниях

Файл:Dipole.gif

Эволюция поля колеблющегося электрического диполя в реальном времени. Диполь находится в точке (60,60) и колеблется по вертикали с частотой 1 рад/с (~0.16 Гц)

Поле точечного диполя, колеблющегося в вакууме, имеет вид

E=3n(n,d)−dR3+3n(n,d˙)−d˙cR2+n(n,d¨)−d¨c2R{\displaystyle \mathbf {E} ={\frac {3\mathbf {n} (\mathbf {n} ,\mathbf {d} )-\mathbf {d} }{R^{3}}}+{\frac {3\mathbf {n} (\mathbf {n} ,{\dot {\mathbf {d} }})-{\dot {\mathbf {d} }}}{cR^{2}}}+{\frac {\mathbf {n} (\mathbf {n} ,{\ddot {\mathbf {d} }})-{\ddot {\mathbf {d} }}}{c^{2}R}}}

B=d˙R2+d¨Rc,n=n,E+dR3{\displaystyle \mathbf {B} =\left=\left},

где n=RR{\displaystyle \mathbf {n} ={\frac {\mathbf {R} }{R}}} — единичный вектор в рассматриваемом направлении, c{\displaystyle c} — скорость света.

Этим выражениям можно придать несколько другую форму, если ввести вектор Герца

Z=−1R⋅d(t−Rc){\displaystyle \mathbf {Z} =-{\frac {1}{R}}\cdot \mathbf {d} \left(t-{\frac {R}{c}}\right)}

Напомним, что диполь покоится в начале координат, так что d{\displaystyle \mathbf {d} } является функцией одной переменной. Тогда

E=−rotrotZ{\displaystyle \mathbf {E} =-\operatorname {rot} \,\operatorname {rot} \,\mathbf {Z} }

B=−1crotZ˙{\displaystyle \mathbf {B} =-{\frac {1}{c}}\operatorname {rot} \,{\dot {\mathbf {Z} }}}

При этом потенциалы поля можно выбрать в виде

A=−Z˙c, ϕ=divZ{\displaystyle \mathbf {A} =-{\frac {\dot {\mathbf {Z} }}{c}},~~\phi =\operatorname {div} \,\mathbf {Z} }

Указанные формулы можно применять всегда, когда применимо дипольное приближение.

Дипольное излучение (излучение в волновой зоне)

Приведённые формулы существенно упрощаются, если размеры системы много меньше длины излучаемой волны, то есть скорости зарядов много меньше c, а поле рассматривается на расстояниях много больших, чем длина волны. Такую область поля называют волновой зоной. Распространяющуюся волну можно в этой области считать практически плоской. Из всех членов в выражениях для E{\displaystyle \mathbf {E} } и B{\displaystyle \mathbf {B} } существенными оказываются только члены, содержащие вторые производные от d{\displaystyle \mathbf {d} }, так как

d˙c≈dλ{\displaystyle {\frac {\dot {\mathbf {d} }}{c}}\approx {\frac {d}{\lambda }}}

d¨c2≈dλ2{\displaystyle {\frac {\ddot {\mathbf {d} }}{c^{2}}}\approx {\frac {d}{\lambda ^{2}}}}

Выражения для полей принимают вид

B=1c2Rd¨,n, B=n,E{\displaystyle \mathbf {B} ={\frac {1}{c^{2}R}},~~\mathbf {B} =}

E=1c2Rd¨,n,n, E=B,n{\displaystyle \mathbf {E} ={\frac {1}{c^{2}R}}\left,\mathbf {n} \right],~~\mathbf {E} =}

В плоской волне интенсивность излучения в телесный угол do{\displaystyle do} равна

dI=cH24πR2do{\displaystyle dI=c{\frac {H^{2}}{4\pi }}R^{2}do},

поэтому для дипольного излучения

dI=14πc3d¨,n2do=d¨24πc3sin2⁡θdo{\displaystyle dI={\frac {1}{4\pi c^{3}}}^{2}do={\frac {{\ddot {d}}^{2}}{4\pi c^{3}}}\sin ^{2}{\theta }do}

где θ{\displaystyle \theta } — угол между векторами d¨{\displaystyle {\ddot {\mathbf {d} }}} и n{\displaystyle \mathbf {n} }. Найдём полную излучаемую энергию. Учитывая, что do=2πsin⁡θdθ{\displaystyle do=2\pi \,\sin {\theta }\,d\theta }, проинтегрируем выражение по dθ{\displaystyle d\theta } от {\displaystyle 0} до π{\displaystyle \pi }. Полное излучение равно

I=23c3d¨2{\displaystyle I={\frac {2}{3c^{3}}}{\ddot {\mathbf {d} }}^{2}}

Укажем спектральный состав излучения. Он получается заменой вектора d¨{\displaystyle {\ddot {\mathbf {d} }}} на его Фурье-компоненту и одновременным умножением выражения на 2. Таким образом:

dEω=4ω43c3|dω|2dω2π{\displaystyle d{\mathcal {E}}_{\omega }={\frac {4\omega ^{4}}{3c^{3}}}\left|\mathbf {d} _{\omega }\right|^{2}{\frac {d\omega }{2\pi }}}

Дипольный момент системы

Файл:DipoleContour.jpg

Эквипотенциальные поверхности электрического диполя

Электрический диполь

Файл:Electric dipole field lines.svg

Силовые линии электрического диполя

Электрический диполь — идеализированная электронейтральная система, состоящая из точечных и равных по абсолютной величине положительного и отрицательного электрических зарядов.

Другими словами, электрический диполь представляет из себя совокупность двух равных по абсолютной величине разноимённых точечных зарядов, находящихся на некотором расстоянии друг от друга

Произведение вектора l→{\displaystyle {\vec {l}}}, проведённого от отрицательного заряда к положительному, на абсолютную величину зарядов q{\displaystyle q\,}, называется дипольным моментом: d→=ql→{\displaystyle {\vec {d}}=q{\vec {l}}}.

Во внешнем электрическом поле E→{\displaystyle {\vec {E}}} на диполь действует момент сил E→×d→{\displaystyle {\vec {E}}\times {\vec {d}}}, который стремится повернуть его так, чтобы дипольный момент развернулся вдоль направления поля.
Потенциальная энергия диполя в электрическом поле равна −E→⋅d→{\displaystyle -{\vec {E}}\cdot {\vec {d}}}.

Вдали от диполя напряжённость его электрического поля убывает с расстоянием R{\displaystyle R} как 1R3{\displaystyle 1/R^{3}}, то есть быстрее, чем у точечного заряда.

Любая электронейтральная система в некотором приближении может рассматриваться как электрический диполь с моментом d→=∑iqir→i{\displaystyle {\vec {d}}=\sum _{i}q_{i}{\vec {r}}_{i}}, где qi{\displaystyle q_{i}\,} — заряд i{\displaystyle i}-го элемента, r→i{\displaystyle {\vec {r}}_{i}} — его радиус-вектор. При этом дипольное приближение будет корректным, если расстояние, на котором изучается электрическое поле системы, велико по сравнению с её характерными размерами.

Магнитный диполь

Магнитный диполь — аналог электрического, который можно представить себе как систему двух «магнитных зарядов» (эта аналогия условна, так как магнитных зарядов, с точки зрения современной электродинамики, не существует). В качестве модели магнитного диполя можно рассматривать небольшую (по сравнению с расстояниями, на которых изучается генерируемое диполем магнитное поле) плоскую замкнутую проводящую рамку площади S{\displaystyle S\,}, по которой течёт ток I{\displaystyle I\,}. При этом магнитным моментом диполя (в системе СГСМ) называют величину μ→=ISn→{\displaystyle {\vec {\mu }}=IS{\vec {n}}}, где n→{\displaystyle {\vec {n}}} — единичный вектор, направленный перпендикулярно плоскости рамки в том направлении, с которого ток в рамке течёт против часовой стрелки.