Потенциал электрического поля — формулы определения, характеристика и единицы измерения

Понятие потенциала

Из курса электродинамики в 10 классе известно, что для определения взаимного влияния электрических зарядов используется понятие напряженности.

Рис. 1. Напряженность электрического поля.

Однако для электротехники такая характеристика поля неудобна. В самом деле, напряженность — это векторная величина, предполагающая движение зарядов в пространстве. Но в электротехнических схемах заряды могут двигаться только по проводникам, направление которых однозначно определено. И имеет значение только движение вдоль проводников. Здесь было бы удобнее рассматривать не векторную, а скалярную характеристику поля.

Для введения такой скалярной характеристики вспомним, что основной задачей электротехники является получение и преобразование энергии. А электрическое поле — потенциально, и работа в нем не зависит от пути, по которому двигался заряд. Важна лишь разница потенциальных энергий в конечных точках траектории.

Все это позволяет ввести специальную энергетическую характеристику электростатического поля — потенциал.

Потенциальная энергия взаимодействия двух зарядов равна:

$$W_{потенц}=k{q_1q_2\over r}$$

Из этой формулы следует, что потенциальная энергия электрического поля пропорциональна заряду, и отношение потенциальной энергии к этому заряду постоянно. Это отношение и есть потенциал $\varphi$:

$$\varphi={W_{потенц}\over q}$$

Как и в случае с потенциальной энергией, конкретная величина потенциала не несет большой информации. Практически всегда используется разность потенциалов между двумя точками. Зная ее, можно рассчитать работу, которую совершает заряд при движении от одной точки к другой.

Понятие потенциала в физике

Из курса физики известно, что работа некоторых сил, например силы тяжести, не зависит от траектории движения тела, а зависит лишь от величины перемещения.

Такие силы и силовые поля, в которых они действуют, называют потенциальными или консервативными.

Сила, действующая на заряд, помещенный в однородное электростатическое поле, также относится к потенциальным и определяется формулой: 

В механике работа определяется как произведение силы на расстояние между точками – началом и концом движения и косинусом угла α между векторами силы и скорости. Аналогично выведем формулу для определения работы электростатического поля при перемещении заряда из одного положения в другое.

Работа зависит от разницы потенциальных энергий в начальной и конечной точке. Тогда работу можно представить как: 

Формула для потенциала одного заряда приведена выше. На практике любое заряженное тело можно разделить на несколько элементов, каждый из которых будет иметь свой потенциал. Тогда потенциал системы, состоящей из двух и более зарядов:

Измерено

Его измерение выполняется в физике, как и в биологии, благодаря вольтметру или осциллографу, которые всегда подключаются в обход или параллельно по отношению к цепи или биполярному объекту, который нужно измерить.

Потенциал всегда определяется в пределах константы. В электричестве принято считать, что в качестве эталона для потенциалов (то есть потенциала, который служит нулем ) мы принимаем потенциал земли (который мы сокращаем до земли ), даже если это не является обязательным требованием. Независимо от выбора, контрольная точка в цепи, потенциал которой зафиксирован на уровне 0 вольт, называется холодной точкой . В зависимости от устройства, он может быть подключен либо к земле (металлический корпус устройства), либо к земле , либо к тому и другому.

Для более практических объяснений, касающихся понятия электрического потенциала, будет ссылка на напряжение в статье .

Потенциал. Разность потенциалов. ЗАДАЧИ с решениями

Формулы, используемые на уроках «Решение задач на тему: Работа перемещения заряда в электрическом поле. Потенциал. Разность потенциалов» для подготовки к ЕГЭ.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача № 1.
 Металлический шар диаметром d заряжен с поверхностной плотностью зарядов σ. Найти потенциал φ этого шара, если он окружен заземленной проводящей сферой, имеющей общий с шаром центр. Диаметр сферы D. Среда — воздух.

Задача № 2.
 Потенциал заряженного шара φ₁ = 300 В. Чему равен потенциал φ₂ электрического поля этого шара в точке, отстоящей на расстоянии l = 50 см от его поверхности, если радиус шара R = 25 см?

Задача № 3.
 Определить потенциал φ точки поля, находящейся на расстоянии а =  9 см от поверхности заряженного шара радиусом R = 1 см, если поверхностная плотность зарядов на шаре σ = 1 • 10–11 Кл/см2. Среда — воздух.

Задача № 4.
 В точке 1 поля точечного заряда-источника потенциал φ₁ = 40 В, а в точке 2 φ₂ = 10 В. Найти потенциал φ в точке М, лежащей посередине между точками 1 и 2 (рис. 3-6). 

Задача № 5.
 В трех вершинах квадрата со стороной а = 20 см находятся заряды q₁ = 1 • 10–8 Кл, q₂ = 2 • 10–8 Кл и q₃ = 2 • 10–8 Кл (рис. 3-7). Определить потенциал φ электрического поля, созданного этими зарядами в четвертой вершине. 

Задача № 6.
 Четыре одинаковых точечных заряда q расположены на одной прямой на расстоянии r друг от друга. Какую работу А надо совершить, чтобы переместить эти заряды в вершины тетраэдра со стороной r? Среда — вакуум.

Задача № 7.
Два одинаково заряженных шарика диаметрами d = 0,5 см каждый расположены на расстоянии l = 2 см между их поверхностями (рис. 3-14). До какого потенциала φ они заряжены, если сила их отталкивания друг от друга F = 2 мкН? Среда — воздух. 

Задача № 8.
 В однородном электрическом поле напряженностью Е = 2 кВ/см переместили заряд q = –20 нКл в направлении силовой линии поля на расстояние d = 10 см. Найти работу поля А, изменение потенциальной энергии поля ΔW_п и напряжение (разность потенциалов) U между начальной и конечной точками перемещения.

Задача № 9.
 Между двумя горизонтальными плоскостями, заряженными разноименно и расположенными на расстоянии d = 5 мм друг от друга, находится в равновесии капелька масла массой 20 нг (нанограмм) (рис. 3-10). Найти число избыточных электронов N на этой капельке. Среда — воздух. Разность потенциалов между плоскостями U = 2 кВ. 

Задача № 10.
 На пластине М поддерживается потенциал φ₁ = +80 В, а на пластине N – φ₂ = –80 В (рис. 3-11, а). Расстояние между пластинами d = 10 см. На расстоянии d₁ = 4 см от пластины М помещают заземленную пластину Р (рис. 3-11, б). Найти изменение напряженности ΔЕ₁ поля на участке МР и изменение напряженности поля ΔЕ₂ на участке PN при этом. Построить графики зависимостей напряженностей Е = Е(х) и потенциала φ = φ(х) от расстояния между точками поля и пластинами. 

Это конспект по теме «Потенциал. Разность потенциалов. ЗАДАЧИ с решениями». Выберите дальнейшие действия:

• Вернуться к списку конспектов по Физике.
• Проверить свои знания по Физике.

Электростатика. Основные понятия. Электрический заряд. Закон сохранения электрического заряда. Закон Кулона. Принцип суперпозиции. Теория близкодействия. Потенциал электрического поля. Конденсатор.

Электрический заряд Q : это физическая величина, характеризующая свойство тел вступать в электрическое взаимодействие. Одноименные заряды отталкиваются, а разноименные заряды притягиваются Элементарный заряд: e=1,6*10-19 Кл это минимальная порция заряда, котрая может передаваться от одного тела к другому (заряд протона или электрона) Электрическое поле: это создаваемый любым электрическим зарядом материальный объект, непрерываный в пространстве, проявляющийся в том, что действет на другие заряды. Проводник: это материал, по которому заряд может свободно перемещаться от одного тела к другому. Диэлектрик: это материал, по которому электрический заряд при обычных условиях перемещаться не может.
Закон сохранения электрического заряда: в замкнутой системе алгебраическая (с учетом знаков +/-) сумма зарядов остается постоянной
Закон Кулона: сила взаимодействия двух точечных зарядов (=кулоновская сила) направлена вдоль прямой, соединяющей заряды, прямо пропорциональна модулю зарядов и обратно пропорциональна квадрату расстояния между ними:
Принцип суперпозиции для электрических зарядов: результирующая сила, действующая на данный заряд q1 со стороны нескольких зарядов q2…..qn, равна геометрической сумме (= векторной сумме) сил F12+….F1n, действующих на данный заряд со стороны каждого из зарядов:
Напряженность электрического поля [В/м]: E (векторная величина) это отношение силы F (векторной величины) с которой поле действует на точечный заряд q (скалярной величины), к этому заряду (с учетом знака заряда): Напряженность электрического поля единичного точечного заряда Q: на расстоянии r от него (напрямую следует из закона Кулона):
Принцип суперпозиции электрических полей: если в данной точке пространства различные заряженные частицы создают электрические поля, напряженности которых E1,E2,….En, то результирующая напряженность электрического поля в этой точке равна векторной сумме отдельных напряжённостей:
Потенциальная энергия: заряда q в однородном электростатическом поле напряженности E: , где d — расстояние до плоскости, где потенциальная энергия принимается равной нулю Потенциал электростатического поля в точке : это отношение потенциальной энергии заряда в поле, к этому заряду (с учетом знака заряда): Вариант 2: это работа по перемещению единичного положительного заряда из данной точки в бесконечность Напряжение = Разность потенциалов между точками: это отношение работы поля при перемещении заряда из начальной точки в конечную к этому заряду ( с учетом знака заряда): Численно (но не по размерности) это работа поля по перемещению единичного положительного заряда из одной точки в другую Связь разности потенциалов и напряженности: в однородном поле: где U это разность потенциалов между точками, которые cвязаны вектором перемещения Δd, совпадающим по направлению с вектором E
Электроемкость двух проводников: это отношение заряда Q одного из проводников к разности потенциалов U между этим проводником и соседним: Конденсатор: это система двух проводников (обкладок конденсатора), разделенных слоем диэлектрика, толщина которого мала по отношению к размерам обкладок Напряженность поля плоского конденсатора: Электроемкость плоского конденсатора: Энергия заряженного конденсатора:

Понятие потенциала, разности потенциалов

С понятием напряжения электрического тока тесно связано понятие «потенциал» , или «разность потенциалов». Хорошо, обратимся снова к нашей водопроводной аналогии.

Наш резервуар находится на возвышенности что позволяет воде беспрепятственно стекать по трубе вниз. Так как бак с водой на высоте, то и потенциал этой точки будет более высоким или более положительным чем тот что находится на уровне земли. Видите что получается?

У нас появилось две точки имеющие разные потенциалы, точнее разную величину потенциала.

Получается, для того чтобы электрический ток мог бежать по проводу, потенциалы не должны быть равны.  Ток бежит от точки с большим потенциалом к точки с меньшим потенциалом.

Помните такое выражение, что ток бежит от плюса к минусу. Так вот это все тоже самое. Плюс это более положительный потенциал а минус более отрицательный.

Кстати а хотите вопрос на засыпку? Что произойдет с током, если величины потенциалов будет периодически меняться местами?

Тогда мы будем наблюдать то как электрический ток меняет свое направление на противоположное каждый раз как потенциалы поменяются. Это получится уже переменный ток. Но его мы пока рассматривать не будем, дабы в голове сформировалось ясное понимание процессов.

Электростатика

Электрический потенциал отдельных положительных и отрицательных точечных зарядов показан в цветном диапазоне от пурпурного (+) до желтого (0) и голубого (-). Круговые контуры — это эквипотенциальные линии. Силовые линии электрического поля оставляют положительный заряд и переходят в отрицательный.

Электрический потенциал вблизи двух противоположных точечных зарядов.

Электрический потенциал в точке r в статическом электрическом поле E определяется линейным интегралом

VE=−∫CE⋅dℓ{\ Displaystyle V _ {\ mathbf {E}} = — \ int _ {C} \ mathbf {E} \ cdot \ mathrm {d} {\ boldsymbol {\ ell}} \,}

где C — произвольный путь, соединяющий точку с нулевым потенциалом с r . Когда ротор ∇ × E равен нулю, линейный интеграл выше не зависит от конкретного выбранного пути C, а только от его конечных точек. В этом случае электрическое поле консервативно и определяется градиентом потенциала:

E=−∇VE.{\ Displaystyle \ mathbf {E} = — \ mathbf {\ nabla} V _ {\ mathbf {E}}. \,}

Тогда по закону Гаусса потенциал удовлетворяет уравнению Пуассона

∇⋅E=∇⋅(−∇VE)=−∇2VE=ρε,{\ displaystyle \ mathbf {\ nabla} \ cdot \ mathbf {E} = \ mathbf {\ nabla} \ cdot \ left (- \ mathbf {\ nabla} V _ {\ mathbf {E}} \ right) = — \ nabla ^ {2} V _ {\ mathbf {E}} = \ rho / \ varepsilon _ {0}, \,}

где ρ является общей плотностью заряда ( в том числе связанного заряда ) и ∇ · обозначает дивергенцию .

Понятие электрического потенциала тесно связано с потенциальной энергией . Пробный заряд Q имеет электрическую потенциальную энергию U _Е , данную

UE=qV.{\ Displaystyle U _ {\ mathbf {E}} = д \, V. \,}

Потенциальная энергия и, следовательно, электрический потенциал определяется только с точностью до аддитивной константы: нужно произвольно выбрать положение, в котором потенциальная энергия и электрический потенциал равны нулю.

Эти уравнения не могут быть использованы , если локонов ∇ × E ≠ 0 , то есть, в случае неконсервативного электрического поля (вызванное изменяющимся магнитным полем , см уравнений Максвелла ). Обобщение электрического потенциала на этот случай описано ниже.

Электрический потенциал из-за точечного заряда

Электрический потенциал, создаваемый зарядом Q, равен V  =  Q / (4πε r ). Различные значения Q будут давать разные значения электрического потенциала V (показано на изображении).

Электрический потенциал, возникающий из точечного заряда Q на расстоянии r от заряда, оказывается равным

VE=14πεQr,{\ displaystyle V _ {\ mathbf {E}} = {\ frac {1} {4 \ pi \ varepsilon _ {0}}} {\ frac {Q} {r}},}

где ε — диэлектрическая проницаемость вакуума . V _E известен как кулоновский потенциал .

Электрический потенциал системы точечных зарядов равен сумме индивидуальных потенциалов точечных зарядов. Этот факт значительно упрощает вычисления, поскольку сложение потенциальных (скалярных) полей намного проще, чем добавление электрических (векторных) полей. В частности, потенциал набора дискретных точечных зарядов q _i в точках r _i становится

VE(r)=14πε∑iqi|r−ri|,{\ displaystyle V _ {\ mathbf {E}} (\ mathbf {r}) = {\ frac {1} {4 \ pi \ varepsilon _ {0}}} \ sum _ {i} {\ frac {q_ {i }} {| \ mathbf {r} — \ mathbf {r} _ {i} |}},}

Где

r{\ displaystyle \ mathbf {r}} это точка, в которой оценивается потенциал.

ri{\ Displaystyle \ mathbf {r} _ {я}} это точка, в которой есть ненулевой заряд.

qi{\ displaystyle q_ {i}} это заряд в точке ri{\ Displaystyle \ mathbf {r} _ {я}}.

и потенциал непрерывного распределения заряда ρ ( r ) принимает вид

VE(r)=14πε∫Rρ(r′)|r−r′|d3r′.{\ displaystyle V _ {\ mathbf {E}} (\ mathbf {r}) = {\ frac {1} {4 \ pi \ varepsilon _ {0}}} \ int _ {R} {\ frac {\ rho ( \ mathbf {r} ‘)} {| \ mathbf {r} — \ mathbf {r}’ |}} d ^ {3} r ‘.}

Где

r{\ displaystyle \ mathbf {r}} это точка, в которой оценивается потенциал.

R{\ displaystyle R} — область, содержащая все точки, в которых плотность заряда отлична от нуля.

r′{\ displaystyle \ mathbf {r} ‘} точка внутри R{\ displaystyle R}.

ρ(r′){\ displaystyle \ rho (\ mathbf {r} ‘)} — плотность заряда в точке r′{\ displaystyle \ mathbf {r} ‘}.

Приведенные выше уравнения для электрического потенциала (и все используемые здесь уравнения) имеют форму, требуемую для единиц СИ . В некоторых других (менее распространенных) системах единиц, таких как CGS-Gaussian , многие из этих уравнений будут изменены.

Ссылки

1. Гольдштейн, Герберт (июнь 1959 г.). Классическая механика . США: Эддисон-Уэсли. п. 383. ISBN. .
2. Гриффитс, Дэвид Дж. Введение в электродинамику . Пирсон Прентис Холл. С. 416–417. ISBN 978-81-203-1601-0.
3. Янг, Хью А .; Фридман, Роджер Д. (2012). Физика Университета Сирса и Земанского с современной физикой (13-е изд.). Бостон: Эддисон-Уэсли. п. 754.
4. «2018 CODATA Значение: электрическая диэлектрическая проницаемость вакуума» . Справочник NIST по константам, единицам и неопределенности . NIST . 20 мая 2019 . Проверено 20 мая 2019 .
5. Bagotskii VS (2006). Основы электрохимии . п. 22. ISBN 978-0-471-70058-6.

Потенциал электрического поля. Разность потенциалов

Потенциал – скалярная физическая величина, равная отношению потенциальной энергии электрического заряда в электростатическом поле к величине этого заряда.

Обозначение – ​\( \varphi \)​, единица измерения в СИ – вольт (В).

Потенциал \( \varphi \) является энергетической характеристикой электростатического поля.

Разность потенциалов численно равна работе, которую совершает электрическая сила при перемещении единичного положительного заряда между двумя точками поля:

Обозначение – ​\( \Delta\varphi \)​, единица измерения в СИ – вольт (В).

Иногда разность потенциалов обозначают буквой ​\( U \)​ и называют напряжением.

Важно!
Разность потенциалов \( \Delta\varphi=\varphi_1-\varphi_2 \), а не изменение потенциала \( \Delta\varphi=\varphi_2-\varphi_1 \). Тогда работа электростатического поля равна:

Важно!
Эта формула позволяет вычислить работу электростатических сил в любом поле. В электростатике часто вычисляют потенциал относительно бесконечно удаленной точки

В этом случае потенциал поля в данной точке равен работе, которую совершают электрические силы при удалении единичного положительного заряда из данной точки в бесконечность

В электростатике часто вычисляют потенциал относительно бесконечно удаленной точки. В этом случае потенциал поля в данной точке равен работе, которую совершают электрические силы при удалении единичного положительного заряда из данной точки в бесконечность.

Потенциал поля точечного заряда ​\( q \)​ в точке, удаленной от него на расстояние ​\( r \)​, вычисляется по формуле:

Для наглядного представления электрического поля используют эквипотенциальные поверхности.

Важно!
Внутри проводящего шара потенциал всех точек внутри шара равен потенциалу поверхности шара и вычисляется по формуле потенциала точечного заряда (​\( r =R \)​, где ​\( R \)​ – радиус шара). Напряженность поля внутри шара равна нулю

Эквипотенциальной поверхностью, или поверхностью равного потенциала, называется поверхность, во всех точках которой потенциал имеет одинаковое значение.

Свойства эквипотенциальных поверхностей

• Вектор напряженности перпендикулярен эквипотенциальным поверхностям и направлен в сторону убывания потенциала.
• Работа по перемещению заряда по эквипотенциальной поверхности равна нулю.

В случае однородного поля эквипотенциальные поверхности представляют собой систему параллельных плоскостей. Для точечного заряда эквипотенциальные поверхности представляют собой концентрические окружности.

Разность потенциалов и напряженность связаны формулой:

Из принципа суперпозиции полей следует принцип суперпозиции потенциалов:

Потенциал результирующего поля равен сумме потенциалов полей отдельных зарядов.

Важно!
Потенциалы складываются алгебраически, а напряженности – по правилу сложения векторов. Решение задач о точечных зарядах и системах, сводящихся к ним, основано на применении законов сохранения, теоремы об изменении кинетической энергии заряда с учетом работы электростатических сил

Решение задач о точечных зарядах и системах, сводящихся к ним, основано на применении законов сохранения, теоремы об изменении кинетической энергии заряда с учетом работы электростатических сил.

Алгоритм решения таких задач:

• установить характер и особенности электростатических взаимодействий объектов системы;
• ввести характеристики (силовые и энергетические) этих взаимодействий, сделать рисунок;
• записать законы сохранения и движения для объектов;
• выразить энергию электростатического взаимодействия через заряды, потенциалы, напряженности;
• составить систему уравнений и решить ее относительно искомой величины;
• проверить решение.

Разность потенциалов

Практическое значение имеет не сам потенциал в точке, а изменение (разница) потенциала φ1 — φ2 , которое не зависит от выбора нулевого уровня отсчета потенциала. Разность потенциалов φ1 — φ2 еще называют напряжением и обозначают латинской буквой U. Тогда формула для работы по перемещению заряда приобретает вид

Напряжение U — это физическая величина, определяемая работой электрического поля по перемещению единичного положительного заряда между двумя точками поля,

Единица разности потенциалов (напряжения), как и потенциала, — вольт,

Поскольку работа сил поля по перемещению заряда зависит только от разности потенциалов, то в случае перемещения заряда с первой эквипотенциальной поверхности на другую (потенциалы которых соответственно φ1 и φ2 ) выполненная полем работа не зависит от траектории этого движения.

Что такое электрический потенциал простыми словами – Все об электричестве

Всем привет, на связи с вами снова Владимир Васильев.  Новогодние празднования подходят к концу, а значить надо готовиться к рабочим будням, с чем вас дорогие друзья и поздравляю! Хех,  только не надо расстраиваться и впадать в депрессию, нужно мыслить позитивно.

Так вот в эти новогодние праздники я как-то размышлял о аудитории моего блога: «Кто он? Кто тот посетитель моего блога, что каждый день заходит почитать мои посты?».  Может быть это прошаренный  спец зашел из любопытства почитать что я тут накалякал?  А может это какой -нибудь доктор радиотехнических наук зашел посмотреть как спаять схему мультивибратора?

Электрический потенциал

Электрический потенциал – это скалярная физическая величина, характеризующая напряжённость поля. Через параметр также выражается электрическое напряжение.

Потенциальная энергия

Изменение электрической потенциальной энергии заряженной частицы рассчитывается по разности потенциалов в каждой из точек. Можно провести аналогию между высотой и потенциалом. Когда у частицы уменьшается потенциал, ее потенциальная энергия уменьшается пропорционально. Однако, в отличие от гравитационной потенциальной энергии , электрическая потенциальная энергия зависит от электрического заряда частицы, а не от ее массы (которая является «гравитационным зарядом»):

Eпезнак равноqV{\ displaystyle E _ {\ mathrm {pe}} = q \, V}

или же :

• Eпе{\ displaystyle E _ {\ mathrm {pe}}}- электрическая потенциальная энергия ,
• V{\ displaystyle V} электрический потенциал,
• q{\ displaystyle q}заряд частицы (положительный или отрицательный).

Слайды и текст этой презентации

Слайд 1Электрическое поле, его характеристики. Поле диполя. Диполь

в однородном и неоднородном электрическом поле. Постоянный

ток, его характеристики и законы. Электропроводность металлов, электролитов, газов

Практическое занятие 7

Слайд 2Любое протяженное заряженное тело – совокупностьточечных зарядов

поле

Можнонаблюдатьс помощьюорганов чувств

Упрощениеописанияэлектрическихвзаимодействий

Слайд 3«Инструмент исследования» электрического поля – пробный (+)

точечный электрический заряд,помещаемый в различные точки пространства

(поля)

Электрическоеполе

На пробный (+) заряд со стороны полядействует сила

Напряженность поля в данной точке

2. Пробный (+) заряд в данной точке обладает потенциальной энергией П:

Потенциал поля в данной точке (нестрого):

Слайд 4Напряженность поля точечного заряда (закон Кулона):направление вектора

напряженности – по направлениюсилы, действующей на (+)

пробный заряд, помещенный в данную точку поля:

модуль:

Принцип суперпозиции (наложения):

Слайд 6Электрическое поле создано двумя точечными зарядами: q1

= 30 нКл и q2 = –50

нКл. Расстояние d между зарядами равно 5 см. Определить напряженность и потенциал электрического поля в точке, находящейся на расстоянии r1 = 3 см от первого и на расстоянии r2 = 4 см от второго зарядов.

СИ:

Слайд 11Оценить электрический заряд Земли (он отрицателен), если

напряженность электрического поля у поверхности Земли Е

= 130 В/м. Радиус Земли 6400 км. Возможно ли путем измерения напряженности (потенциала) электрического поля в различных точках пространства определить распределение электрического заряда, создающего поле, в пространстве?

СИ:

Слайд 12Электрон перемещается между точками с разностью потенциалов

1В. Найти работу сил поля и приращение

кинетической энергии электрона.

СИ:

Электростатические силы –консервативные:

Закон сохранения энергии для системы, в которойдействуют только консервативные силы:

того, чтобы сообщить скорость v2 =30 Мм/с

первоначально покоящемуся электрону?

СИ:

Слайд 15Определить потенциал φ поля, создаваемого диполем с

электрическим моментом р=4 пКл·м на расстоянии r

= 10 см от центра диполя, в направлении, составляющем угол α = 60˚ с вектором электрического момента.

СИ:

ре=4·10-12 Кл·м

r = 0,10 м

Слайд 16Мгновенное распределение (+) и (-) зарядов в

теле(следствие процесса жизнедеятельности):Суммарный заряд тела = 0Полученная

простая система издвух равных по модулю, противоположных по знаку зарядов – электрический диполь.

Электрический момент диполя:

Слайд 17Точечные электрические заряды располагаются вдоль оси ОХ.

Значения зарядов и их координаты: q1 =

0,10мКл, q2 = 0,20 мКл, q3 = 0,30 мКл, q4 = -0,05мКл, q5 = — 0,20 мКл , q6 = — 0,35 мКл; х1 = 10 мм, х2 = 20 мм, х3 = 30 мм, х4 = 0 мм, х5 = -10 мм, х6 = — 50 мм. Оценить значение дипольного момента данного распределения зарядов.

Может ли данная система моделироваться электрическим диполем?

Слайд 20Двойной фосфолипидный слой уподобляет биологическую мембрану конденсатору.

Вещество мембраны представляет собой диэлектрик с диэлектрической

проницаемостью ε. Разность потенциалов между поверхностями мембраны равна U при толщине мембраны d. Оценить электроемкость участка  мембраны площадью S и напряженность электрического поля в ней.

Слайд 22Средняя мощность разряда электрического сома Р =

8 Вт при напряжении U = 360

В. Время разряда t = 0,13 мс. Определить электроемкость органов сома.

СИ:

t = 0,13·10-3 с

Энергия электрического поля,аккумулированная сомом:

Мощность, выделяемая при разряде:

Слайд 23Оценить, какое количество одновалентных ионов должно перейти

из цитоплазмы в межклеточную жидкость для создания

потенциала покоя φм≈ -120 мВ? Принять площадь поверхности клетки S = 10-9 м2; удельную электроемкость мембраны (на единицу площади) Суд = 10-2 Ф/м2.

СИ:

Δφ = 0,120 В

Заряд мембранного конденсатора:

Количество одновалентных ионов:

Вступление

Объект может иметь электрический заряд . Помещенный в электрическое поле , такой заряженный объект испытывает силу . Если объект заряжен положительно, сила действует в направлении вектора электрического поля в том месте, где находится объект; если его заряд отрицательный, сила действует в противоположном направлении. Действующая сила равна произведению заряда на электрическое поле.

Электрический потенциал (или более просто потенциал ) в точке электрического поля соответствует работе должно быть сделано , чтобы транспортировать единичный положительный заряд от бесконечности до этого момента (электрический потенциал на бесконечности существа по определению равно 0).

Сила и потенциал напрямую связаны. Когда объект движется в направлении силы, которая приводит его в движение, его кинетическая энергия увеличивается; например, гравитационная потенциальная энергия объекта на вершине башни выше, чем на земле. Когда объект падает, его кинетическая энергия увеличивается и преобразуется в тепло или тепловую энергию .

Электрическое поле (в отсутствие переменного магнитного поля ) разделяет с гравитационным силовым полем (гравитацией) то свойство, что потенциальная энергия зависит только от положения в поле: сила, действующая на объект, не зависит от силы внутренние свойства этого объекта (например, масса или заряд) и его положение, и подчиняется математическим правилам. Мы говорим, что электрическая сила консервативна .

Вот почему мы обычно используем для иллюстрации понятия электрического потенциала аналогию с водотоком реки; потенциал каждой точки соответствует ее высоте, в то время как разница в высоте (разность уровней) соответствует разнице потенциалов.

Разность потенциалов (или напряжение при отсутствии индукционных явлений внешнего происхождения) — это алгебраическая величина (она может быть положительной, отрицательной или нулевой); часто отмечается U .

Поэтому мы можем написать:

UВBзнак равноV(В)-V(B){\ Displaystyle U _ {\ mathrm {AB}} = V (\ mathrm {A}) -V (\ mathrm {B})}

ΔVзнак равноVокончательный-Vисходный{\ displaystyle \ Delta V = V _ {\ text {final}} — V _ {\ text {initial}}}

или же :

V(В){\ Displaystyle V (\ mathrm {A})}и обозначают электрический потенциал в A и B  ;V(B){\ Displaystyle V (\ mathrm {B})}

UВB{\ Displaystyle U _ {\ mathrm {AB}}}и обозначим разность потенциалов между А и B .ΔV{\ displaystyle \ Delta V}

Оно представлено на схемах подключения стрелки от точки B до точки A .

Конструктор ЗНАТОК 320-Znat «320 схем»

Конструктор ЗНАТОК 320-Znat «320 схем» — это инструмент, который позволит получить знания в области электроники и электротехники а также достичь понимания процессов происходящих в проводниках.

Конструктор представляет собой набор полноценных радиодеталей имеющих спец. конструктив,  позволяющий их монтаж без помощи паяльника. Радиокомпоненты монтируются на специальную плату — основание, что позволяет в конечном итоге получить вполне функциональные радиоконструкции.

Используя этот конструктор можно собрать до 320 различных схем,  для построения которых есть развернутое и красочное руководство.  А если подключить фантазию в этот творческий процесс то можно получить бесчисленное количество различных радиоконструкций и   научиться анализировать их работу. Этот опыт я считаю очень важен и для многих он может оказаться бесценным.

Вот несколько примеров того, что Вы можете сделать благодаря этому конструктору:

Летающий пропеллер;
Лампа,включаемая хлопком в ладоши или струей воздуха;
Управляемые звуки звездных войн, пожарной машины или скорой помощи;
Музыкальный вентилятор;
Электрическое световое ружье;
Изучение азбуки Морзе;
Детектор лжи;
Автоматический уличный фонарь;
Мегафон;
Радиостанция;
Электронный метроном;
Радиоприемники, в том числе FM диапазона;
Устройство, напоминающее о наступлении темноты или рассвета;
Сигнализация о том, что ребенок мокрый;
Защитная сигнализация;
Музыкальный дверной замок;
Лампы при параллельном и последовательном соединении;
Резистор как ограничитель тока;
Заряд и разряд конденсатора;
Тестер электропроводимости;
Усилительный эффект транзистора;
Схема Дарлингтона.

P.S. У нас тут есть своеобразный жлобометр — жадный не заметит соцкнопки, а  щедрый делится с друзьями.

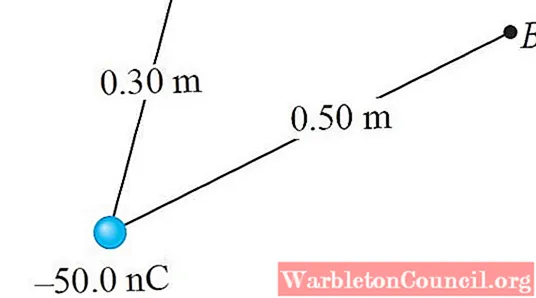
Упражнение решено

Нагрузка Q = — 50,0 нКл находится на расстоянии 0,30 м от точки К и 0,50 м от точки B, как показано на следующем рисунке. Ответьте на следующие вопросы:

а) Каков потенциал в А, создаваемый этим зарядом?

б) А каков потенциал у B?

c) Если заряд q перемещается от A к B, через какую разность потенциалов он перемещается?

г) Согласно предыдущему ответу, его потенциал увеличивается или уменьшается?

д) Если q = — 1,0 нКл, каково изменение его электростатической потенциальной энергии при перемещении от A к B?

е) Какую работу совершает электрическое поле, создаваемое Q, при перемещении испытательного заряда от А к В?

Фотоэффект

Фотоэффект называется способность металла испускать часть своих электронов под воздействием света. Если проводник или металл находятся в состоянии покоя, то в их структуре происходит свободное перемещение электронов. Причем эти частицы все время пытаются сместиться к поверхности тела и покинуть его пределы. Препятствием для свободного покидания электронами данного тела служат положительно заряженные ионы. Ведь именно этими положительными зарядами и удерживаются электроны. Открыл фотоэффект в 1887 г. немецкий ученый Генрих Р. Герц. Кроме того над изучением фотоэффекта довольно долго работали такие ученые — А.Г. Столетов и Ф. Леонард.