Rc-цепь. дифференцирующие и интегрирующие rc-цепи

Справочная информация

ДокументыЗаконыИзвещенияУтверждения документовДоговораЗапросы предложенийТехнические заданияПланы развитияДокументоведениеАналитикаМероприятияКонкурсыИтогиАдминистрации городовПриказыКонтрактыВыполнение работПротоколы рассмотрения заявокАукционыПроектыПротоколыБюджетные организацииМуниципалитетыРайоныОбразованияПрограммыОтчетыпо упоминаниямДокументная базаЦенные бумагиПоложенияФинансовые документыПостановленияРубрикатор по темамФинансыгорода Российской Федерациирегионыпо точным датамРегламентыТерминыНаучная терминологияФинансоваяЭкономическаяВремяДаты2015 год2016 годДокументы в финансовой сферев инвестиционной

Дифференцирующая RC-цепь.

Из названия цепи, в принципе, уже понятно, что за элементы входят в ее состав – это конденсатор и резистор И выглядит она следующим образом:

Работа данной схемы основана на том, что ток, протекающий через конденсатор, прямо пропорционален скорости изменения напряжения, приложенного к нему:

i = C\medspace\frac{dU_c}{dt}

Напряжения в цепи связаны следующим образом (по закону Кирхгофа):

u_{out} = u_{in}\medspace-\medspace u_c

В то же время, по закону Ома мы можем записать:

u_{out} = i R = C R\medspace\frac{dU_c}{dt}

Выразим u_c из первого выражения и подставим во второе:

u_{out} = C R\medspace\frac{dU_c}{dt} = C R\medspace(\frac{dU_{in}}{dt}\medspace-\medspace \frac{dU_{out}}{dt}\medspace)
u_{out} = C R\medspace\frac{dU_{in}}{dt}\medspace-\medspace C R\medspace\frac{dU_{out}}{dt}

При условии, что C R\medspace\frac{dU_{out}}{dt} << u_{out} (то есть скорость изменения напряжения низкая) мы получаем приближенную зависимость для напряжения на выходе:

u_{out} \approx C R\medspace\frac{dU_{in}}{dt}

Таким образом, цепь полностью оправдывает свое название, ведь напряжение на выходе представляет из себя дифференциал входного сигнала. Но возможен еще и другой случай, когда C R\medspace\frac{dU_{out}}{dt} >> u_{out} (быстрое изменение напряжения). При выполнении этого равенства мы получаем такую ситуацию:

C R\medspace\frac{dU_{in}}{dt} = C R\medspace\frac{dU_{out}}{dt}

То есть: U_{out} \approx U_{in}.

Можно заметить, что условие C R\medspace\frac{dU_{out}}{dt} << u_{out} будет лучше выполняться при небольших значениях произведения C R, которое называют постоянной времени цепи:

\tau = R C

Давайте разберемся, какой смысл несет в себе эта характеристика цепи Заряд и разряд конденсатора происходит по экспоненциальному закону:

u = U_0\medspace e^{-t/\tau}

Здесь U_0 – напряжение на заряженном конденсаторе в начальный момент времени. Теперь посмотрим, каким будет значение напряжения по истечении времени \tau:

U_{\tau} = U_0\medspace e^{-\tau/\tau} = U_0\medspace e^{-1} \approx 0.37\medspace U_0

Напряжение на конденсаторе уменьшится до 37% от первоначального. Таким образом, \tau – это время, за которое конденсатор:

при заряде – зарядится до 63%
при разряде – разрядится на 63% (разрядится до 37%)

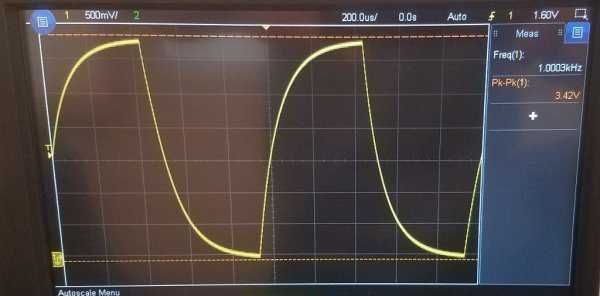
С постоянной времени цепи мы разобрались, давайте вернемся к дифференцирующей RC-цепи. Теоретические аспекты функционирования мы разобрали, так что давайте посмотрим, как она работает на практике. А для этого попробуем подавать на вход какой-нибудь сигнал и посмотрим, что получится на выходе. В качестве примера, подадим на вход последовательность прямоугольных импульсов:

А вот как выглядит осциллограмма выходного сигнала (второй канал – синий цвет):

Что же мы тут видим?

Большую часть времени напряжение на входе неизменно, а значит его дифференциал равен 0 (производная константы = 0). Именно это мы и видим на графике, значит RC-цепь выполняет свою дифференцирующую функцию. А с чем же связаны всплески на выходной осциллограмме? Все просто – при “включении” входного сигнала происходит процесс зарядки конденсатора, то есть по цепи проходит ток зарядки и напряжение на выходе максимально. А затем по мере протекания процесса зарядки ток уменьшается по экспоненциальному закону до нулевого значения, а вместе с ним уменьшается напряжение на выходе, ведь оно равно U_{out} = i R. Давайте увеличим масштаб осциллограммы и тогда мы получим наглядную иллюстрацию процесса зарядки:

При “отключении” сигнала на входе дифференцирующей цепи происходит аналогичный переходный процесс, но только вызван он не зарядкой, а разрядкой конденсатора.

В данном случае постоянная времени цепи у нас имеет небольшую величину, поэтому цепь хорошо дифференцирует входной сигнал. По нашим теоретическим расчетам, чем больше мы будем увеличивать постоянную времени, тем больше выходной сигнал будет похож на входной. Давай проверим это на практике! Будем увеличивать сопротивление резистора, что и приведет к росту \tau:

Тут даже не надо ничего комментировать – результат налицо Мы подтвердили теоретические выкладки, проведя практические эксперименты, так что давайте переходить к следующему вопросу – к интергрирующим RC-цепям.

Цепь RC:

Цепи RC (резистор конденсатор цепь) будут состоять из конденсатора и резистор соединены последовательно или параллельно напряжения или источник тока. Эти типы схем также называются RC-фильтрами или RC- цепями, поскольку они чаще всего используются в приложениях фильтрации. RC-цепь может использоваться для создания некоторых грубых фильтров, таких как фильтры нижних и верхних частот и полосовые фильтры. Схема первого порядка RC будет состоять только из одного резистора и одного конденсатора, и мы будем анализировать то же самое в этом руководстве

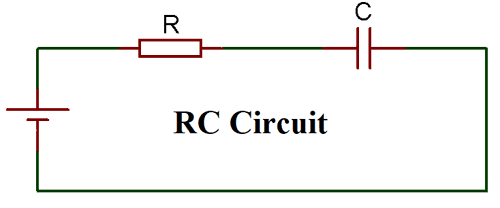
Чтобы понять RC-схему, давайте создадим базовую схему на Proteus и подключим нагрузку через осциллограф, чтобы проанализировать его поведение. Схема вместе с формой волны приведена ниже.

Мы подключили нагрузку (лампочку) с известным сопротивлением 1 кОм последовательно с конденсатором 470 мкФ, чтобы сформировать RC-цепь. Схема питается от батареи 12 В, а переключатель используется для замыкания и размыкания цепи. Форма волны измеряется через лампочку нагрузки и показана желтым цветом на изображении выше.

Первоначально, когда переключатель разомкнут, максимальное напряжение (12 В) появляется на резистивной нагрузке лампочки (Vr), и напряжение на конденсаторе будет нулевым. Когда переключатель замкнут, напряжение на резисторе упадет до нуля, а затем, когда конденсатор заряжается, напряжение вернется к максимуму, как показано на графике.

Время, необходимое для зарядки конденсатора, определяется формулой T = 5Ƭ, где “Ƭ” представляет tou (постоянная времени).

Давайте посчитаем время, за которое наш конденсатор заряжается в цепи.

Ƭ = RC = (1000 * (470 * 10 ^ -6)) = 0,47 секунды T = 5 = (5 * 0,47) T = 2,35 секунды.

Мы подсчитали, что время, необходимое для зарядки конденсатора, составит 2,35 секунды, то же самое можно проверить на графике выше. Время, необходимое для достижения Vr от 0 В до 12 В, равно времени, необходимому для зарядки конденсатора от 0 В до максимального напряжения. График иллюстрируется курсорами на изображении ниже.

Аналогичным образом мы также можем рассчитать напряжение на конденсаторе в любой момент времени и ток через конденсатор в любой момент времени, используя следующие формулы

V (t) = V _B (1 — e -t / RC) I (t) = I _o (1 — e -t / RC)

Где V _B — напряжение батареи, а I _o — выходной ток схемы. Значение t — это время (в секундах), в течение которого необходимо рассчитать значение напряжения или тока конденсатора.

Цепь RL:

RL цепи (резистор Индуктор цепи) будет состоять из индуктора и резистора снова соединены последовательно или параллельно. Последовательная цепь RL будет управляться источником напряжения, а параллельная цепь RL будет управляться источником тока. Цепи RL обычно используются в качестве пассивных фильтров, схема RL первого порядка только с одной катушкой индуктивности и одним конденсатором показана ниже.

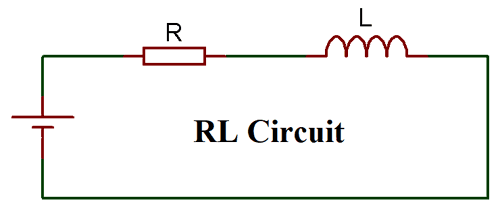
Точно так же в цепи RL мы должны заменить конденсатор на индуктор. Предполагается, что лампочка действует как чисто резистивная нагрузка, а сопротивление лампы установлено на известное значение 100 Ом.

Когда цепь разомкнута, напряжение на резистивной нагрузке будет максимальным, а когда переключатель замкнут, напряжение от батареи распределяется между индуктором и резистивной нагрузкой. Катушка индуктивности заряжается быстро, и, следовательно, на резистивной нагрузке R произойдет резкое падение напряжения.

Время, необходимое для зарядки индуктора, можно рассчитать по формуле T = 5Ƭ, где “Ƭ” представляет tou (постоянная времени).

Давайте посчитаем время, за которое наша катушка индуктивности заряжается в цепи. Здесь мы использовали индуктивность номиналом 1 мГн и резистор номиналом 100 Ом.

Ƭ = L / R = (1 * 10 ^ -3) / (100) = 10 ^ -5 секунд T = 5Ƭ = (5 * 10 ^ -5) = 50 * 10 ^ -6 T = 50 u секунд.

Точно так же мы также можем рассчитать напряжение на индукторе в любой момент времени и ток через индуктор в любой момент времени, используя следующие формулы:

V (t) = V _B (1 — e -tR / L) I (t) = I _o (1 — e -tR / L)

Где V _B — напряжение батареи, а I _o — выходной ток схемы. Значение t — это время (в секундах), в течение которого должно быть вычислено значение напряжения или тока индуктора.

Определение постоянной времени. Переходные процессы в R-L-C-цепи.

Как отмечалось в предыдущей лекции, линейная цепь охвачена единым переходным процессом. Поэтому в рассматриваемых цепях с одним накопителем энергии (катушкой индуктивности или конденсатором) – цепях первого порядка – постоянная времени будет одной и той же для всех свободных составляющих напряжений и токов ветвей схемы, параметры которых входят в характеристическое уравнение.

Общий подход к расчету переходных процессов в таких цепях основан на применении теоремы об активном двухполюснике: ветвь, содержащую накопитель, выделяют из цепи, а оставшуюся часть схемы рассматривают как активный двухполюсник А (эквивалентный генератор) (см. рис.1, а) со схемой замещения на рис. 1,б.

Совершенно очевидно, что постоянная времени здесь для цепей с индуктивным элементом определяется, как:

и с емкостным, как:

где — входное сопротивление цепи по отношению к зажимам 1-2 подключения ветви, содержащей накопитель энергии.

Например, для напряжения на конденсаторе в цепи на рис. 2 можно записать

где в соответствии с вышесказанным

Переходные процессы при подключении последовательнойR-L-C-цепи к источнику напряжения

Рассмотрим два случая:

Согласно изложенной в предыдущей лекции методике расчета переходных процессов классическим методом для напряжения на конденсаторе в цепи на рис. 3 можно записать

(1)

Тогда для первого случая принужденная составляющая этого напряжения

(2)

Характеристическое уравнение цепи

решая которое, получаем

В зависимости от соотношения параметров цепи возможны три типа корней и соответственно три варианта выражения для свободной составляющей:

1. или , где — критическое сопротивление контура, меньше которого свободный процесс носит колебательный характер.

В этом случае

(3)

2. — предельный случай апериодического режима.

В этом случае и

(4)

3. — периодический (колебательный) характер переходного процесса.

В этом случае и

(5)

где — коэффициент затухания; — угловая частота собственных колебаний; — период собственных колебаний.

Для апериодического характера переходного процесса после подстановки (2) и (3) в соотношение (1) можно записать

Для нахождения постоянных интегрирования, учитывая, что в общем случае и в соответствии с первым законом коммутации , запишем для t=0 два уравнения:

решая которые, получим

Тогда ток в цепи

и напряжение на катушке индуктивности

На рис. 4 представлены качественные кривые , и , соответствующие апериодическому переходному процессу при .

Для критического режима на основании (2) и (4) можно записать

Для колебательного переходного процесса в соответствии с (2) и (5) имеем

Для нахождения постоянных интегрирования запишем

На рис. 5представлены качественные кривые и , соответствующие колебательному переходному процессу при .

При подключении R-L-C-цепи к источнику синусоидального напряжения для нахождения принужденных составляющих тока в цепи и напряжения на конденсаторе следует воспользоваться символическим методом расчета, в соответствии с которым

Здесь также возможны три режима:

1. ;

Наибольший интерес представляет третий режим, связанный с появлением во время переходного процесса собственных колебаний с частотой . При этом возможны, в зависимости от соотношения частот собственных колебаний и напряжения источника, три характерные варианта: 1 — ; 2 — ; 3 — , — которые представлены на рис. 6,а…6,в соответственно.

Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
Теоретические основы электротехники. Учеб. для вузов. В трех т. Под общ. ред. К.М.Поливанова. Т.1. К.М.Поливанов. Линейные электрические цепи с сосредоточенными постоянными. –М.: Энергия- 1972. –240с.

Как можно определить постоянную времени в цепи с одним накопителем энергии по осциллограмме тока или напряжения в какой-либо ветви?
Определить, какой процесс: заряд или разряд конденсатора в цепи на рис. 2 – будет происходить быстрее?

Дифференцирующая RC цепь

Еще одно ругательное слово, которое пришло с математики — дифференцирующий. Башка начинает сразу же болеть от одного только их произношения. Но, куда деваться? Электроника и математика неразлучные друзья.

А вот и сама дифференциальная цепочка

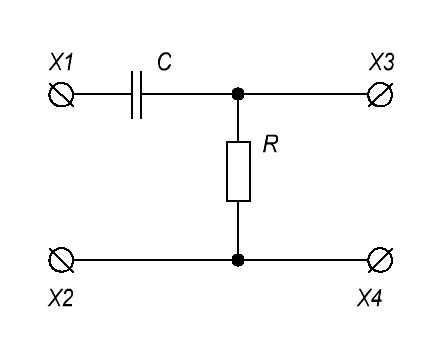
В схеме мы только переставили резистор и конденсатор местами

Ну а теперь проведем также все опыты, как мы делали с интегрирующей цепью. Для начала подаем на вход дифференциальной цепи низкочастотный двухполярный меандр с частотой в 1,5 Герца и с размахом в 5 Вольт. Желтый сигнал — это сигнал с генератора частоты, красный — с выхода дифференциальной цепочки:

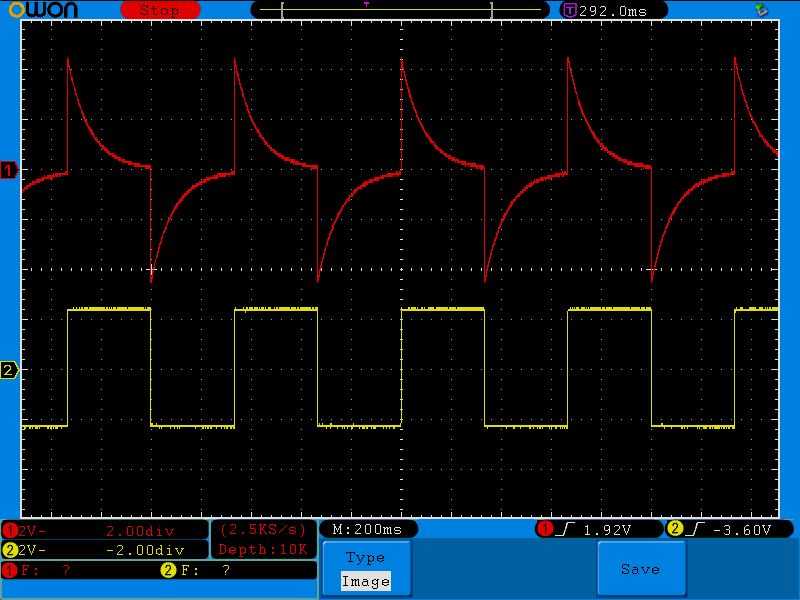
Как вы видите, конденсатор успевает почти полностью разрядится, поэтому у нас получилась вот такая красивая осциллограмма.

Давайте увеличим частоту до 10 Герц

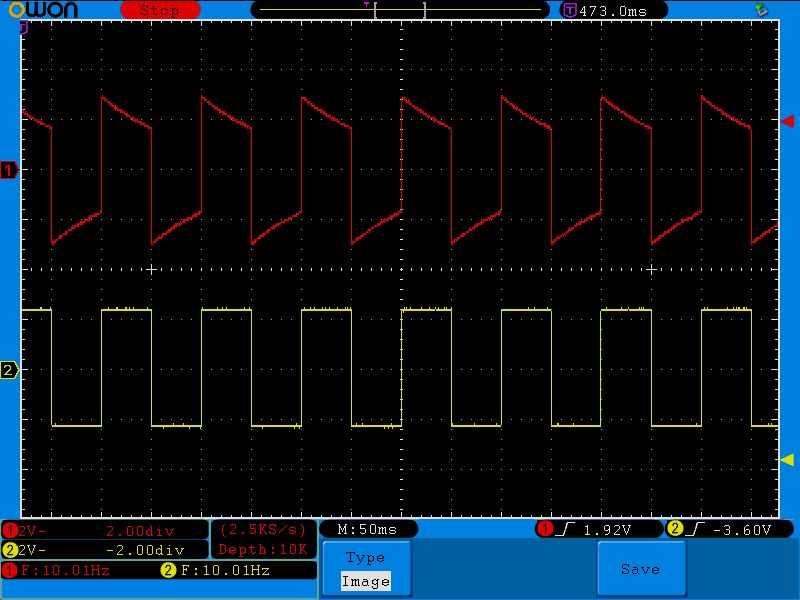
Как видите, конденсатор не успевает разрядиться, как уже приходит новый импульс.

Сигнал в 100 Герц сделал кривую разряда еще менее заметной.

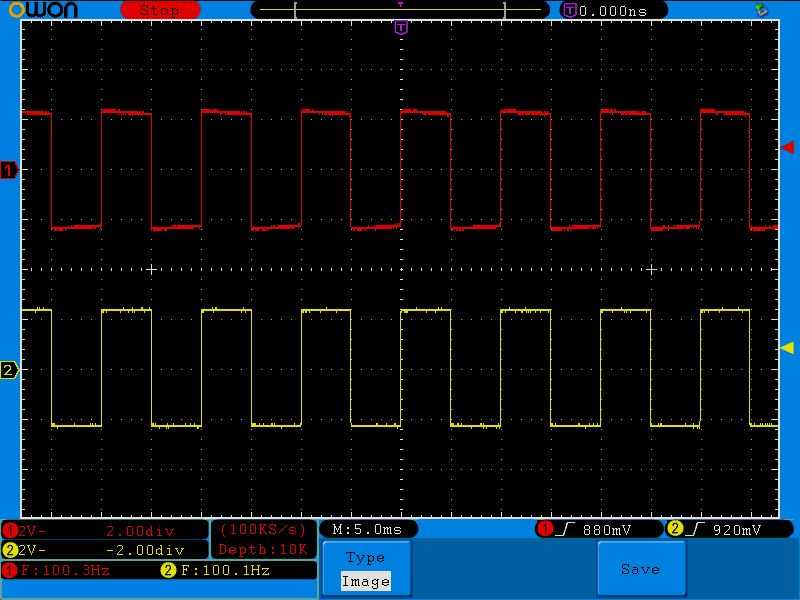
Ну и добавим частоту до 1 Килогерца

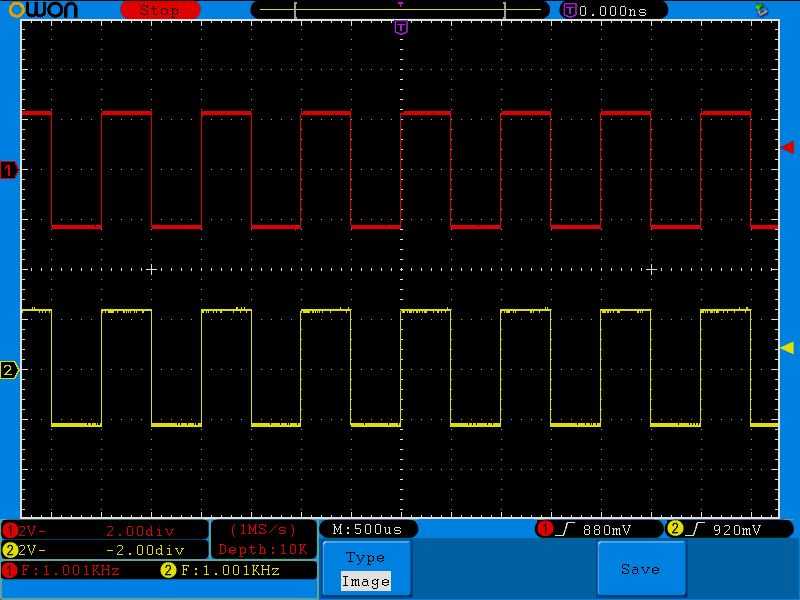
Какой на входе, такой и на выходе С такой частотой конденсатор вообще не успевает разряжаться, поэтому вершинки выходных импульсов гладкие и ровные.

Но и на этом тоже ништяки не заканчиваются.

Давайте я подниму входной сигнал над «уровнем моря», то есть выведу его в положительную часть полностью. Смотрим, что получается на выходе (красный сигнал)

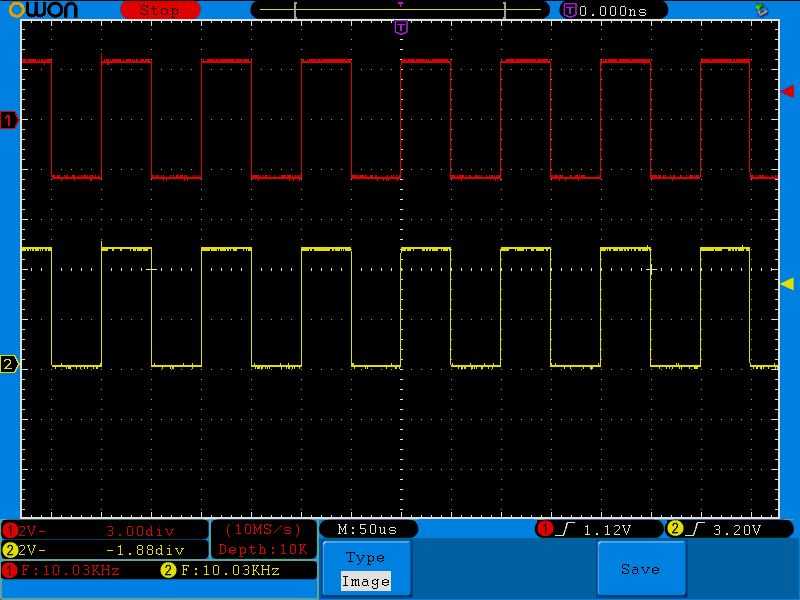
Ничего себе, красный сигнал по форме и по положению остался таким же, посмотрите — в нем нет постоянной составляющей, как в желтом сигнале, который мы подавали из нашего генератора функций.

Могу даже желтый сигнал вывести в отрицательную область, но на выходе мы все равно получим переменную составляющую сигнала без всяких хлопот:

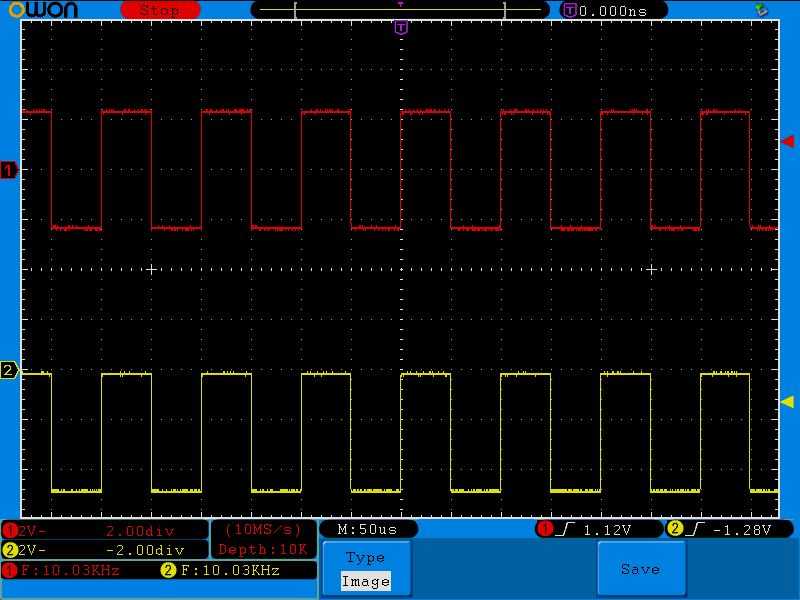
Да и вообще пусть сигнал будет с небольшой отрицательной постоянной составляющей, все равно на выходе мы получим переменную составляющую:

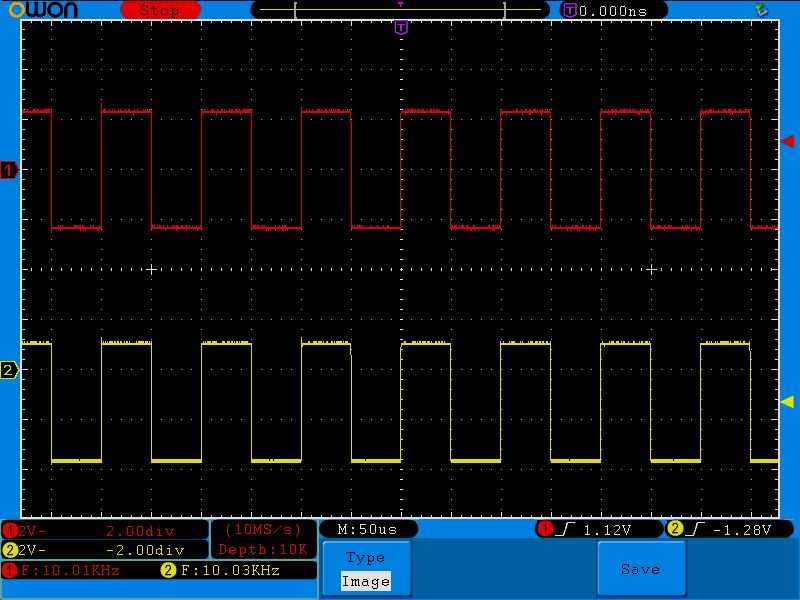
Все то же самое касается и любых других сигналов:

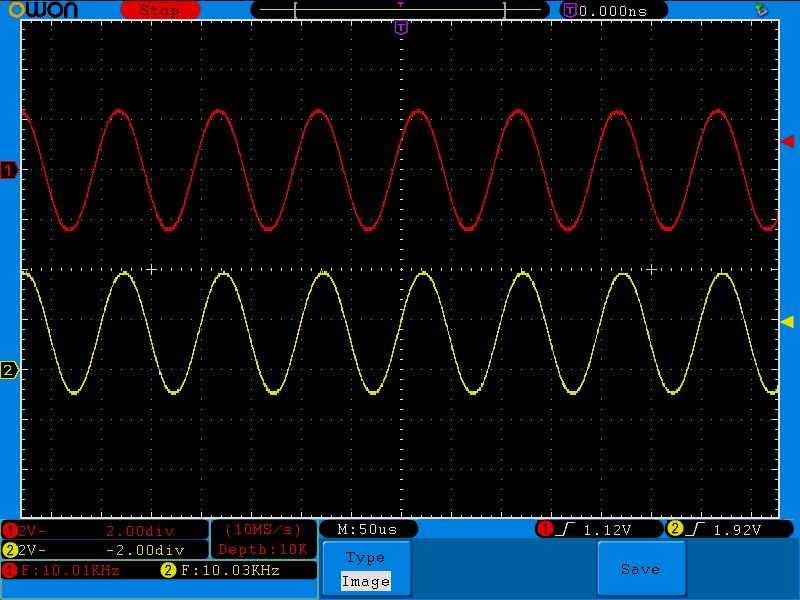
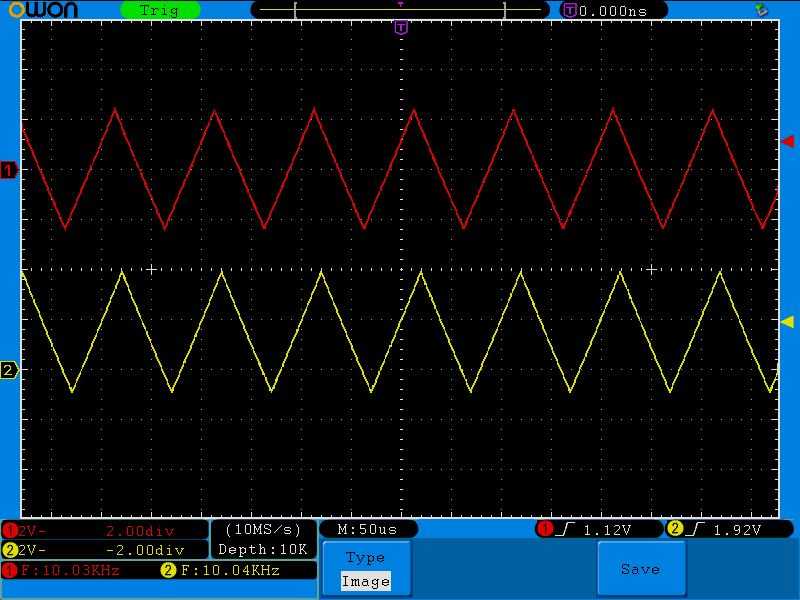
В результате опытов мы видим, что основная функция дифференциальной цепи — это выделение переменной составляющей из сигнала, который содержит в себе как переменную, так и постоянную составляющую. Иными словами — выделение переменного тока из сигнала, который состоит из суммы переменного тока и постоянного тока.

Почему так происходит? Давайте разберемся. Рассмотрим нашу дифференциальную цепь:

Если внимательно рассмотреть эту схему, то мы можем увидеть тот же самый делитель напряжения, как и в интегрирующей цепи. Конденсатор — частотно-зависимый радиоэлемент. Итак, если подать сигнал с частотой в 0 Герц (постоянный ток), то у нас конденсатор тупо зарядится и потом вообще перестанет пропускать через себя ток. Цепь будет в обрыве. Но если мы будем подавать переменный ток, то и через конденсатор он тоже начнет проходить. Чем больше частота — тем меньше сопротивление конденсатора. Следовательно, весь переменный сигнал будет падать на резисторе, с которого мы как раз и снимаем сигнал.

Но если мы будем подавать смешанный сигнал, то есть переменный ток + постоянный ток, то на выходе мы получим просто переменный ток. В этом мы с вами уже убеждались на опыте. Почему так произошло? Да потому что конденсатор не пропускает через себя постоянный ток!

Видео «Как работает RC-цепь РЕАЛЬНО. Понятное объяснение»

Уравнение колебаний в контуре без активного сопротивления

Уравнение, которое описывает процесс изменения заряда в $LC$ контуре, имеет вид:

где $\frac{1}{LC}={\omega }_0$ — собственная частота $LC$ — контура. Решением уравнения (9) служит функция:

Из (10) видно, что заряд на обкладках конденсатора изменяется по гармоническому закону с частотой ${\omega }_0$.

Пример 1

Задание: Запишите функцию зависимости напряжения на конденсаторе от времени ($U(t)$) после замыкания ключа на рис. 4. Считать, что конденсатор был заряжен до напряжения $U_0$.

Рисунок 4.

Решение:

Используем второе правило Кирхгофа, запишем, что после того как ключ в цепи замкнули, выполняется равенство:

где $U_R$ — напряжение на сопротивлении, $U_C$ — напряжение на конденсаторе. При этом можно положить, что:

где $I_C,I_R$ токи, текущие через конденсатор и сопротивление. Используем выражения (1.2) преобразуем уравнение (1.1), получим:

Решение уравнения (1.3) запишем в виде:

Постоянную А найден их начального условия задачи ($U_C\left(0\right)=U_0$), следовательно А=$U_0$.

Ответ: $U_C\left(t\right)=U_0exp\left(-\frac{t}{RC}\right).$

Пример 2

Задание: Приведите пример, как получить в примере 1 режим зарядки и разрядки конденсатора?

Решение:

Заданный режим можно получить, если в качестве источника постоянного напряжения использовать генератор прямоугольных импульсов (поставить его на место ключа рис. 4). При этом ЭДС источника ($\varepsilon (t$)) должна выглядеть как:

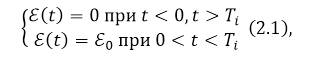Рисунок 5.

где $T_i$ — длительность импульса, причем это время должно быть существенно больше, чем время релаксации для того, чтобы напряжение на конденсаторе успело стать равным ${{\mathcal E}}_0$.

Дифференциальное уравнение [ править ]

Основная статья: теория систем LTI

Системы LTI первого порядка характеризуются дифференциальным уравнением

τ d V d т + V знак равно ж ( т ) {\ Displaystyle \ тау {\ гидроразрыва {dV} {dt}} + V = f (t)}

где τ представляет собой экспоненциальную константу затухания, а V является функцией времени t

V знак равно V ( т ) . {\ Displaystyle V = V (t).}

Правая часть — это вынуждающая функцияf (t ), описывающая внешнюю движущую функцию времени, которую можно рассматривать каквход системы , на которыйV (t ) являетсяответом или выходом системы. Классические примеры дляf (t ) :

Функция Хевисайда , часто обозначается U

(т ) : ты ( т ) знак равно { 0 , т < 0 1 , т ≥ 0 {\displaystyle u(t)={\begin{cases}0,&t<0\\1,&t\geq 0\end{cases}}} импульсная функция , часто обозначается б

(т ) , а также функция синусоидальной входного сигнала: f ( t ) = A sin ⁡ ( 2 π f t ) {\displaystyle f(t)=A\sin(2\pi ft)} или же

f ( t ) = A e j ω t , {\displaystyle f(t)=Ae^{j\omega t},}

где A — амплитуда вынуждающей функции, f — частота в герцах, а ω = 2 π f

— частота в радианах в секунду.

Пример решения

Пример решения дифференциального уравнения с начальным значением V

0 и без функции принуждения: V ( t ) = V o e − t / τ {\displaystyle V(t)=V_{o}e^{-t/\tau }} куда

V o = V ( t = 0 ) {\displaystyle V_{o}=V(t=0)}

это начальное значение V . Таким образом, отклик представляет собой экспоненциальный спад с постоянной времени τ .

Обсуждение

Предполагать

V ( t ) = V 0 e − t / τ {\displaystyle V(t)=V_{0}e^{-t/\tau }} .

Такое поведение называется «убывающей» экспоненциальной функцией. Время τ (тау) называется «постоянной времени» и может использоваться (как в этом случае), чтобы указать, насколько быстро экспоненциальная функция затухает.

Здесь:

t = время (обычноt > 0 в технике управления)V 0 = начальное значение (см. «Особые случаи» ниже).

Конкретные случаи

1) Пусть ; тогда и так t = 0 {\displaystyle t=0} V = V 0 e 0 {\displaystyle V=V_{0}e^{0}} V = V 0 {\displaystyle V=V_{0}} 2) Пусть ; тогда t = τ {\displaystyle t=\tau } V = V 0 e − 1 ≈ 0.37 V 0 {\displaystyle V=V_{0}e^{-1}\approx 0.37V_{0}} 3) Пусть , и так V = f ( t ) = V 0 e − t / τ {\displaystyle V=f(t)=V_{0}e^{-t/\tau }} lim t → ∞ f ( t ) = 0 {\displaystyle \lim _{t\to \infty }f(t)=0} 4) Пусть ; тогда t = 5 τ {\displaystyle t=5\tau } V = V 0 e − 5 ≈ 0.0067 V 0 {\displaystyle V=V_{0}e^{-5}\approx 0.0067V_{0}} После периода в одну постоянную времени функция достигает e

−1 = примерно 37% от своего начального значения. В случае 4 после пяти постоянных времени функция достигает значения менее 1% от исходного. В большинстве случаев этот порог в 1% считается достаточным, чтобы предположить, что функция упала до нуля — как показывает опыт, в технике управления стабильной системой является система, которая демонстрирует такое общее затухающее поведение.

Дифференцирующие цепи

Довольно часто в электронике вообще, а в импульсной в частности требуется преобразовать один вид импульсов в другой (например, прямоугольный преобразовать в треугольный). Для этой цели используют различные схемы, в основе которых простейшие RC- и RL-цепи. Такие цепи называются дифференцирующими и интернирующими цепями. Для начала рассмотрим дифференцирующие цепи, которые показаны на изображении ниже.

Своё название дифференцирующие цепи получили от того, что напряжение на выходе такой цепи пропорционально производной входного напряжения, а нахождение производной в математике называется дифференцирование. В случае RC-цепи напряжение снимается с резистора, а в случае RL-цепи – с индуктивности.

Простейшие .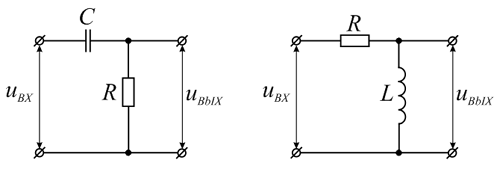

В настоящее время большинство дифференцирующих цепей основаны на RC-цепях, поэтому будем рассматривать их, но все основные выкладки соответствуют также и RL-цепям.

Рассмотрим, как дифференцирующая цепь будет реагировать на прямоугольный импульс. Прямоугольный импульс представляет собой как бы два скачка напряжения. Реакцию RC-цепи на скачкообразное изменение напряжения рассматривалась выше, а в случае прямоугольного импульса выходное напряжение с дифференцирующей цепи будет в виде двух коротких импульсов различной полярности, длительность которых соответствует 3τ = 3RC и 3τ = 3L/R, в случае RL-цепи.

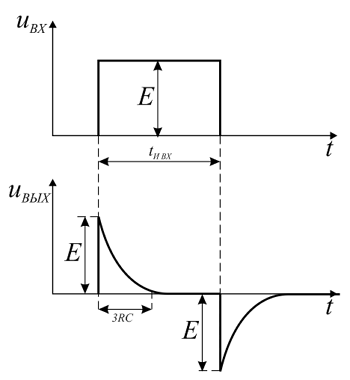
Реакция дифференцирующей цепи на прямоугольный импульс.

Из величины и формы выходного напряжения можно сделать вывод, что дифференциальные цепи вполне могут применяться для уменьшения длительности импульсов, что довольно часто применяется на практике и ранее такие цепи иногда называли укорачивающими.

Синтез

Иногда требуется синтезировать RC-схему из заданной рациональной функции в s . Чтобы синтез пассивных элементов был возможен, функция должна быть положительно-действительной функцией . Для синтеза в виде RC-цепи все критические частоты ( полюса и нули ) должны быть на отрицательной действительной оси и чередоваться между полюсами и нулями с равным количеством каждого из них. Кроме того, критическая частота, ближайшая к началу координат, должна быть полюсом, если предположить, что рациональная функция представляет собой импеданс, а не полную проводимость.

Синтез может быть осуществлен с помощью модификации синтеза Фостера или синтеза Кауэра, используемого для синтеза цепей LC . В случае синтеза Кауэра получится лестничная сеть из резисторов и конденсаторов.

Частота среза

Постоянная временит{\ Displaystyle \ тау}связан с частотой среза f _c , альтернативным параметром RC-цепи, соотношением

тзнак равнорСзнак равно12πфс{\ displaystyle \ tau = RC = {\ frac {1} {2 \ pi f_ {c}}}}

или, что то же самое,

фсзнак равно12πрСзнак равно12πт{\ displaystyle f_ {c} = {\ frac {1} {2 \ pi RC}} = {\ frac {1} {2 \ pi \ tau}}}

где сопротивление в омах и емкость в фарадах дает постоянную времени в секундах или частоту среза в Гц.

Короткие условные уравнения, использующие значение для106(2π){\ Displaystyle 10 ^ {6} / (2 \ пи)}

f _c в Гц = 159155 / τ в мкс

τ в мкс = 159155 / f _c в Гц

Другие полезные уравнения:

время нарастания (от 20% до 80%)тр≈1,4т≈0,22фс{\ displaystyle t_ {r} \ приблизительно 1,4 \ тау \ приблизительно {\ frac {0,22} {f_ {c}}}}

время нарастания (от 10% до 90%)тр≈2.2т≈0,35фс{\ displaystyle t_ {r} \ приблизительно 2,2 \ тау \ приблизительно {\ frac {0,35} {f_ {c}}}}

В более сложных схемах, состоящих из более чем одного резистора и/или конденсатора, метод постоянной времени холостого хода обеспечивает способ аппроксимации частоты среза путем вычисления суммы нескольких постоянных времени RC.

Постоянная времени электрической цепи — что это такое и где используется

Природе свойственны периодические процессы: день сменяет ночь, теплое время года сменяется холодным и т. д. Период этих событий почти постоянен и поэтому может быть строго определен. Кроме того, мы вправе утверждать, что приведенные в качестве примера периодические природные процессы не являются затухающими, по крайней мере по отношению к продолжительности жизни одного человека.

Однако в технике, а в электротехнике и в электронике — особенно, далеко не все процессы являются периодическими и незатухающими. Обычно какой-нибудь электромагнитный процесс сначала возрастает, а затем убывает. Часто дело ограничивается лишь фазой начала колебания, которое так и не успевает толком набрать размах.

Сплошь и рядом в электротехнике можно встретить так называемые экспоненциальные переходные процессы, суть которых заключается в том, что система просто стремится придти к какому-то равновесному состоянию, которое в конце концов выглядит как состояние покоя. Такой переходный процесс может быть как нарастающим, так и спадающим.

Внешняя сила сначала выводят динамическую систему из состояния равновесия, а затем не препятствует естественному возврату данной системы к ее исходному состоянию. Эта последняя фаза и есть так называемый переходный процесс, которому свойственна определенная длительность. Кроме того процесс выведения системы из равновесия также является переходным процессом с характерной длительностью.

Так или иначе, постоянной времени переходного процесса мы называем его временную характеристику, определяющую время, через которое некоторый параметр данного процесса изменится в «е» раз, то есть увеличится или уменьшится примерно в 2,718 раз по сравнению с состоянием, принятым за исходное.

Рассмотрим для примера электрическую цепь, состоящую из источника постоянного напряжения, конденсатора и резистора. Подобного рода цепь, где резистор включен последовательно с конденсатором, называется интегрирующей RC-цепью.

Если в начальный момент времени подать на такую цепь питание, то есть установить на входе некоторое постоянное напряжение Uвх, то Uвых — напряжение на конденсаторе, начнет по экспоненте нарастать.

Через время t1 напряжение на конденсаторе достигнет 63,2% от напряжения на входе. Так вот, промежуток времени от начального момента до t1 – это и будет постоянная времени данной RC-цепи.

Данную константу цепи называют «тау», она измеряется в секундах, а обозначают ее соответствующей греческой буквой. Численно для RC-цепи она равна R*C, где R выражается в омах, а С — в фарадах.

Связь постоянной времени с полосой пропускания

Пример реакции системы на функцию форсирования синусоидальной волны. Ось времени в единицах постоянной времени τ{displaystyle au}. Отклик затухает и становится простой синусоидальной волной.

Частотная характеристика системы в зависимости от частоты в единицах ширины полосы ж_{3 дБ}. Отклик нормализуется до нулевого значения частоты, равного единице, и падает до 1 / √2 в полосе пропускания.

Предположим, что функция принуждения выбрана синусоидальной, поэтому:

τdVdт+V=ж(т)=Аеjωт.{displaystyle au {dV over dt} + V = f (t) = Ae ^ {jomega t}.}

(Отклик на входную реальную косинусную или синусоидальную волну можно получить, взяв действительную или мнимую часть конечного результата в силу Формула Эйлера.) Общее решение этого уравнения для времен т ≥ 0 с, полагая V (t = 0) = V является:

V(т)=Vе−тτ+Ае−тττ∫тdт′ ет′τеjωт′{displaystyle V (t) = V_ {0} e ^ {- t / au} + {Ae ^ {- t / au} над au} int _ {0} ^ {t}, dt ‘e ^ {t’ / au} e ^ {jomega t ‘}}

=Vе−тτ+1τjω+1τА(еjωт−е−тτ).{displaystyle = V_ {0} e ^ {- t / au} + {frac {1 / au} {jomega + 1 / au}} Aleft (e ^ {jomega t} -e ^ {- t / au} ight) .}

В течение долгого времени убывающие экспоненты становятся незначительными и устойчивое состояние раствор или долгосрочное решение:

V∞(т)=1τjω+1τАеjωт.{displaystyle V_ {infty} (t) = {frac {1 / au} {jomega + 1 / au}} Ae ^ {jomega t}.}

Величина этого ответа:

|V∞(т)|=А1τ(ω2+(1τ)2)12=А11+(ωτ)2.{displaystyle | V_ {infty} (t) | = A {frac {1} {au left (omega ^ {2} + (1 / au) ^ {2} ight) ^ {1/2}}} = A { гидроразрыв {1} {sqrt {1+ (omega au) ^ {2}}}}.}

По соглашению, полоса пропускания этой системы — это частота, на которой | V_∞|2 падает до половины значения, или где ωτ = 1. Это обычный пропускная способность условное обозначение, определяемое как частотный диапазон, в котором мощность падает менее чем наполовину (не более −3 дБ). Используя частоту в герцах, а не в радианах / с (ω = 2πж):

ж3dB=12πτ.{displaystyle f_ {3dB} = {frac {1} {2pi au}}.}

Обозначение ж_{3 дБ} проистекает из выражения власти в децибелы и наблюдение, что половинная мощность соответствует падению значения | V_∞| на коэффициент 1 / √2 или на 3 децибела.

Таким образом, постоянная времени определяет полосу пропускания этой системы.

Бизнес и финансы

БанкиБогатство и благосостояниеКоррупция(Преступность)МаркетингМенеджментИнвестицииЦенные бумагиУправлениеОткрытые акционерные обществаПроектыДокументыЦенные бумаги — контрольЦенные бумаги — оценкиОблигацииДолгиВалютаНедвижимость(Аренда)ПрофессииРаботаТорговляУслугиФинансыСтрахованиеБюджетФинансовые услугиКредитыКомпанииГосударственные предприятияЭкономикаМакроэкономикаМикроэкономикаНалогиАудитМеталлургияНефтьСельское хозяйствоЭнергетикаАрхитектураИнтерьерПолы и перекрытияПроцесс строительстваСтроительные материалыТеплоизоляцияЭкстерьерОрганизация и управление производством